viewFourthOrderTensor

Below is a demonstration of the features of the viewFourthOrderTensor2D function

Contents

clear; close all; clc;

Syntax

viewFourthOrderTensor(C,numDigits,fontSizeIm,fontSize);

Description

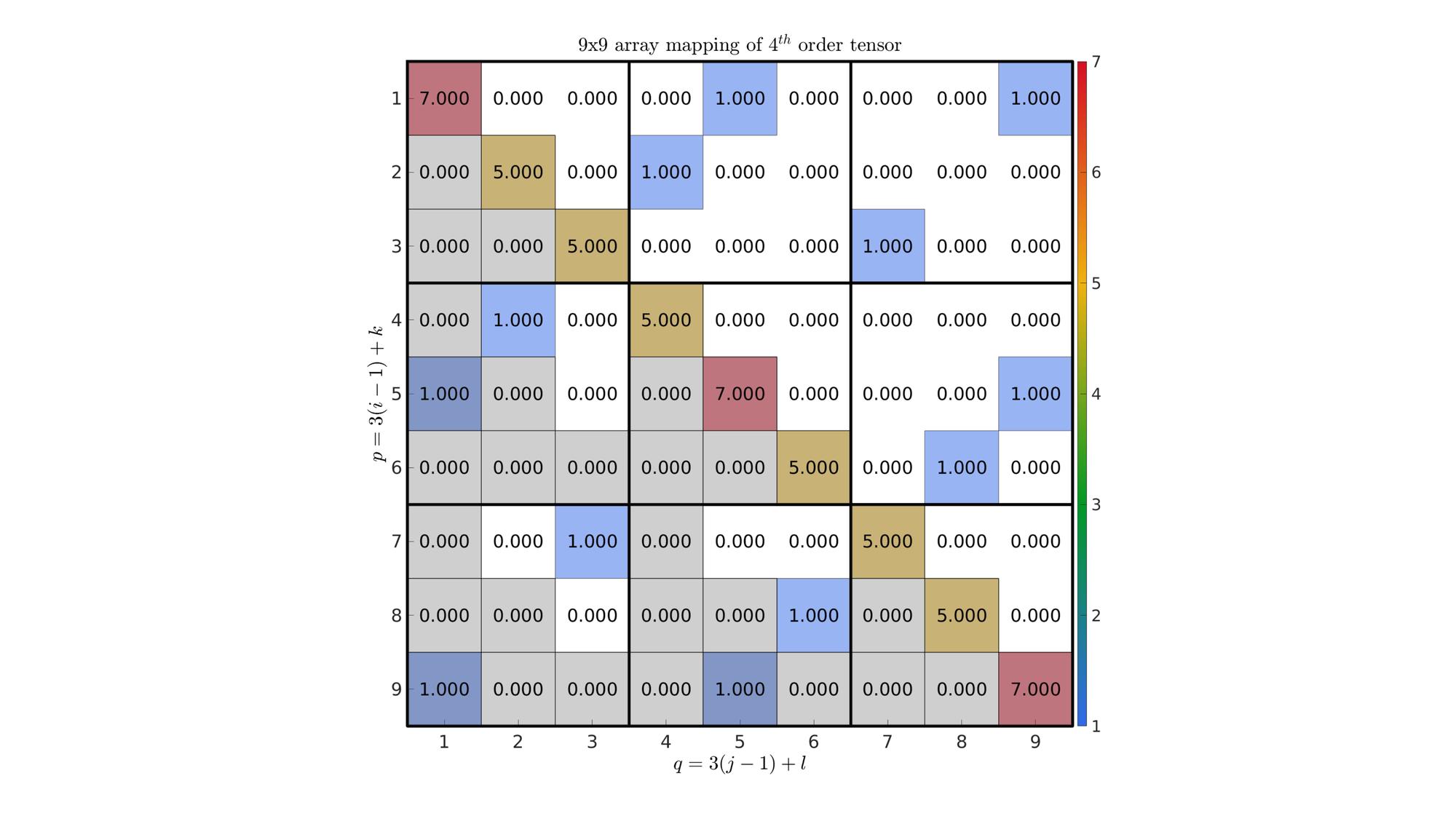
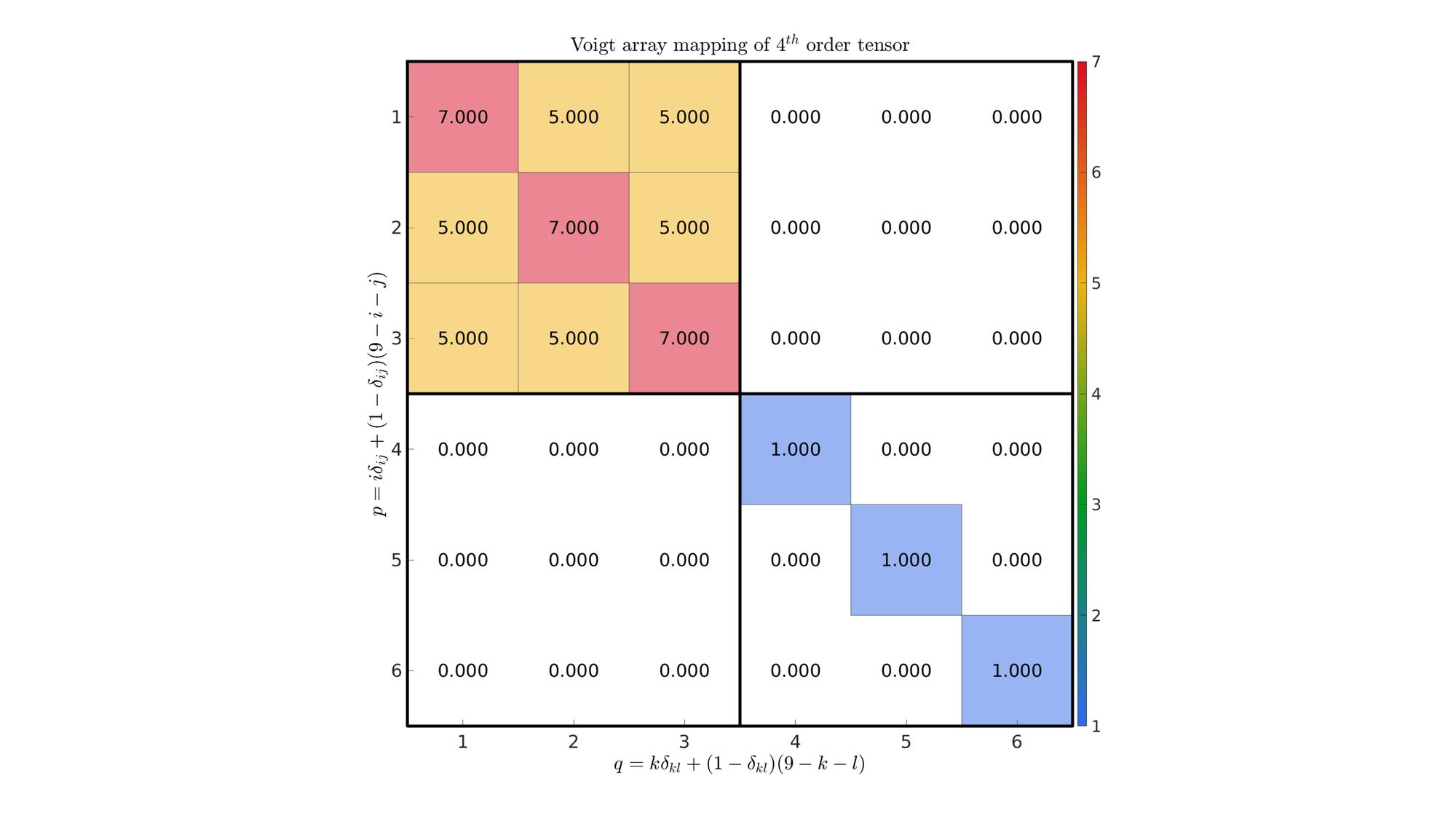
This function creates the 9x9 and the 6x6 (aka Voigt) array mappings for 3D 4th order input tensor C. The function can take up to 4 inputs:

Examples

Viewing fourth-order stiffness tensors

Creating the stiffness tensor for Hooke's law of linear elasticity

%Constructing 4th order base tensor set
I=eye(3,3); %The 2nd order identity tensor
II1=dyadicProduct(I,I,1); %4th order base tensor 1
II3=dyadicProduct(I,I,3); %4th order base tensor 3

%Parameters for Hooke's law
mu=1; %The shear modulus
lambda=5; %The lambda lame parameter
C=lambda.*II1+2.*mu.*II3; %Construct 4th order stiffness tensor

Visualizing the tensor using viewFourthOrderTensor

viewFourthOrderTensor(C); %Visualize tensor C
%
% %% Viewing fourth-order stiffness tensors with symbolic variables
%
% syms mu lambda; %Create symbolic Lame parameters
% C=lambda.*II1+2.*mu.*II3; %Construct 4th order stiffness tensor
%
% %%
% % Visualizing the tensor using |viewFourthOrderTensor|
%
% numDigits=0;
% fontSizeIm=25;
% fontSize=50;
% viewFourthOrderTensor(C,numDigits,fontSizeIm,fontSize); %Visualize tensor C

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2019 Kevin Mattheus Moerman

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2019a