truncatePolyhedra

Below is a demonstration of the features of the truncatePolyhedra function

Contents

Syntax

[FC,VC,CC]=truncatePolyhedra(F,V,w);

Description

This function computes the truncated form of the input solid as specified by the input faces (F), vertices (V), and the truncation factor (w). The output is the patch data (faces, vertices, and color/face labels) for the truncated solid. The truncation factor ranges between 0 and 1. If unspecified or empty the default value is: w=tan(pi/(size(F,2)*2))/tan(pi/(size(F,2))); which provides the uniform truncation.

Examples

clear; close all; clc;

Truncating a solid

Creating a platonic solid which will be truncated

[V,F]=platonic_solid(1,1); %Get a tetrahedron, the first platonic solid
C=zeros(size(F,1),1); %Create color data for visualization

Truncating a platonic solid

[FC,VC,CC]=truncatePolyhedra(F,V);

Visualizing result

cFigure;
subplot(1,2,1);hold on;
title('Normal solid');
gpatch(F,V,C,'k',1,1);
axisGeom;
camlight headlight;
caxis([0 1]);

subplot(1,2,2);hold on;
title('Truncated solid');
gpatch(F,V,'kw','k',0.25,1);
gpatch(FC,VC,CC,'k',1,1);
axisGeom;
camlight headlight;
caxis([0 1]);

colormap(gjet(2));
drawnow;

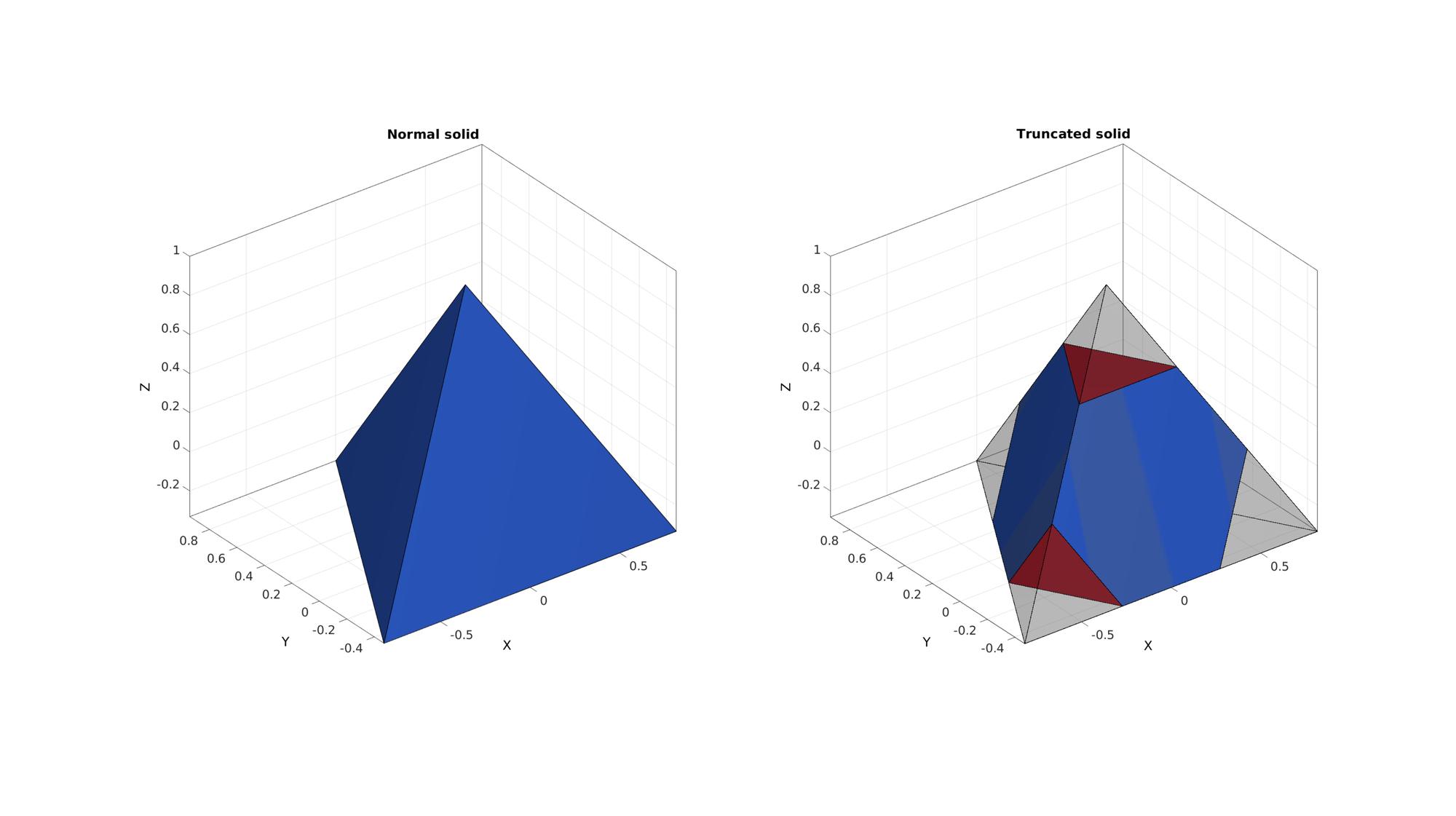
Demonstration of truncation for all platonic solids

cFigure;
for q=1:1:5
    [V,F]=platonic_solid(q,1);
    C=zeros(size(F,1),1);
    [FC,VC,CC]=truncatePolyhedra(F,V);

    subplot(3,5,q);hold on;
    gpatch(F,V,C,'k',1,1);
    axisGeom;
    camlight headlight;
    caxis([0 1]);
    axis off;

    subplot(3,5,q+5);hold on;
    gpatch(FC,VC,CC,'k',1,1);
    axisGeom;
    camlight headlight;
    caxis([0 1]);
    axis off;

    [FC,VC,CC]=truncatePolyhedra(F,V,0);

    subplot(3,5,q+10);hold on;
    gpatch(FC,VC,CC,'k',1,1);
    axisGeom;
    camlight headlight;
    caxis([0 1]);
    axis off;

end
colormap(gjet(2));
drawnow;

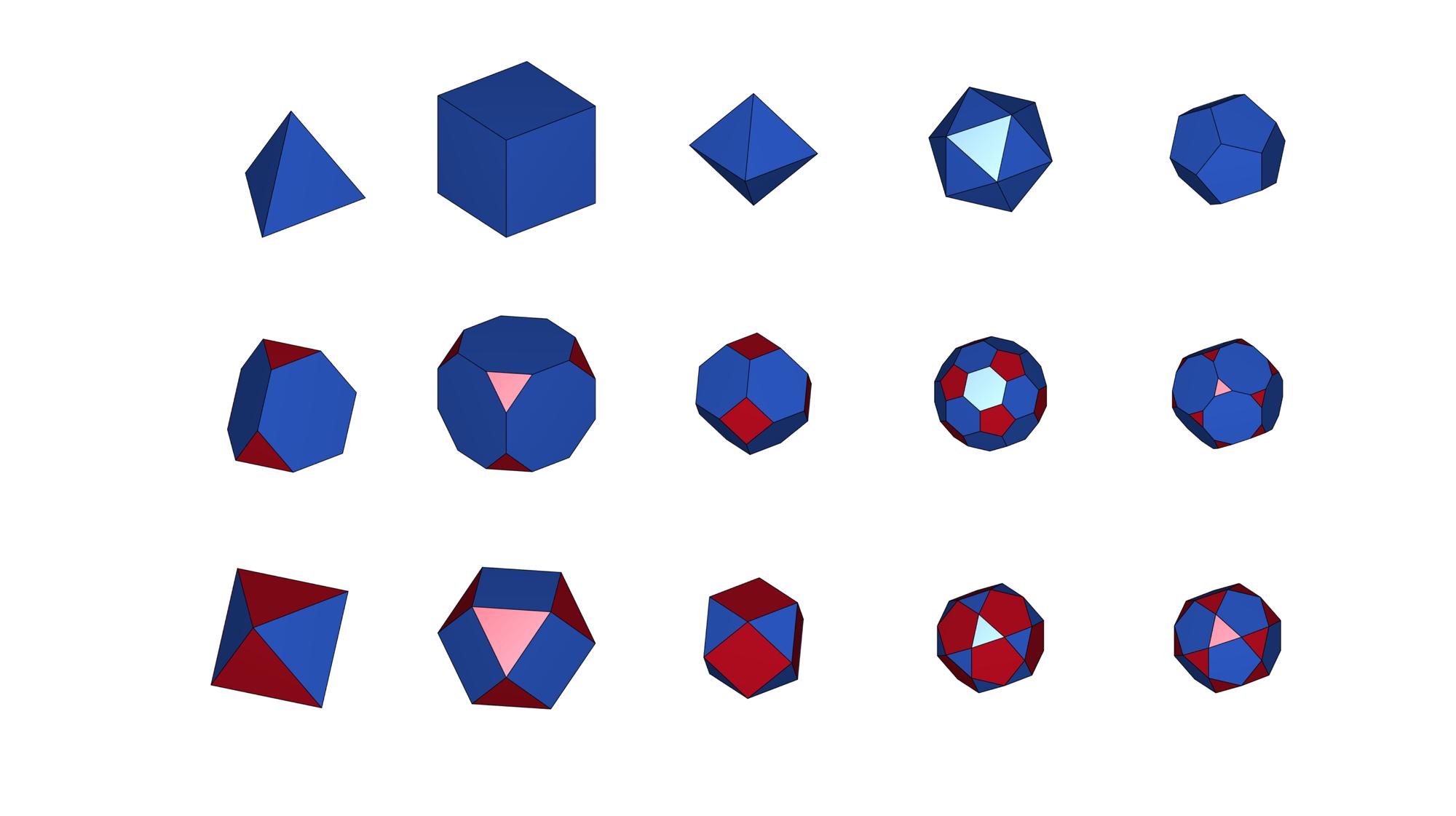
Truncating a general closed surface

% Creating a triangulated sphere
[F,V]=geoSphere(2,1);
C=zeros(size(F,1),1); %Create color data for visualization

Truncating the solid solid

[FC,VC,CC]=truncatePolyhedra(F,V);

Visualizing result

cFigure;
subplot(1,2,1);hold on;
title('Normal solid');
gpatch(F,V,C,'k',1,1);
axisGeom;
camlight headlight;
caxis([0 1]);

subplot(1,2,2);hold on;
title('Truncated solid');
gpatch(FC,VC,CC,'k',1,1);
axisGeom;
camlight headlight;
caxis([0 1]);

colormap(gjet(2));
drawnow;

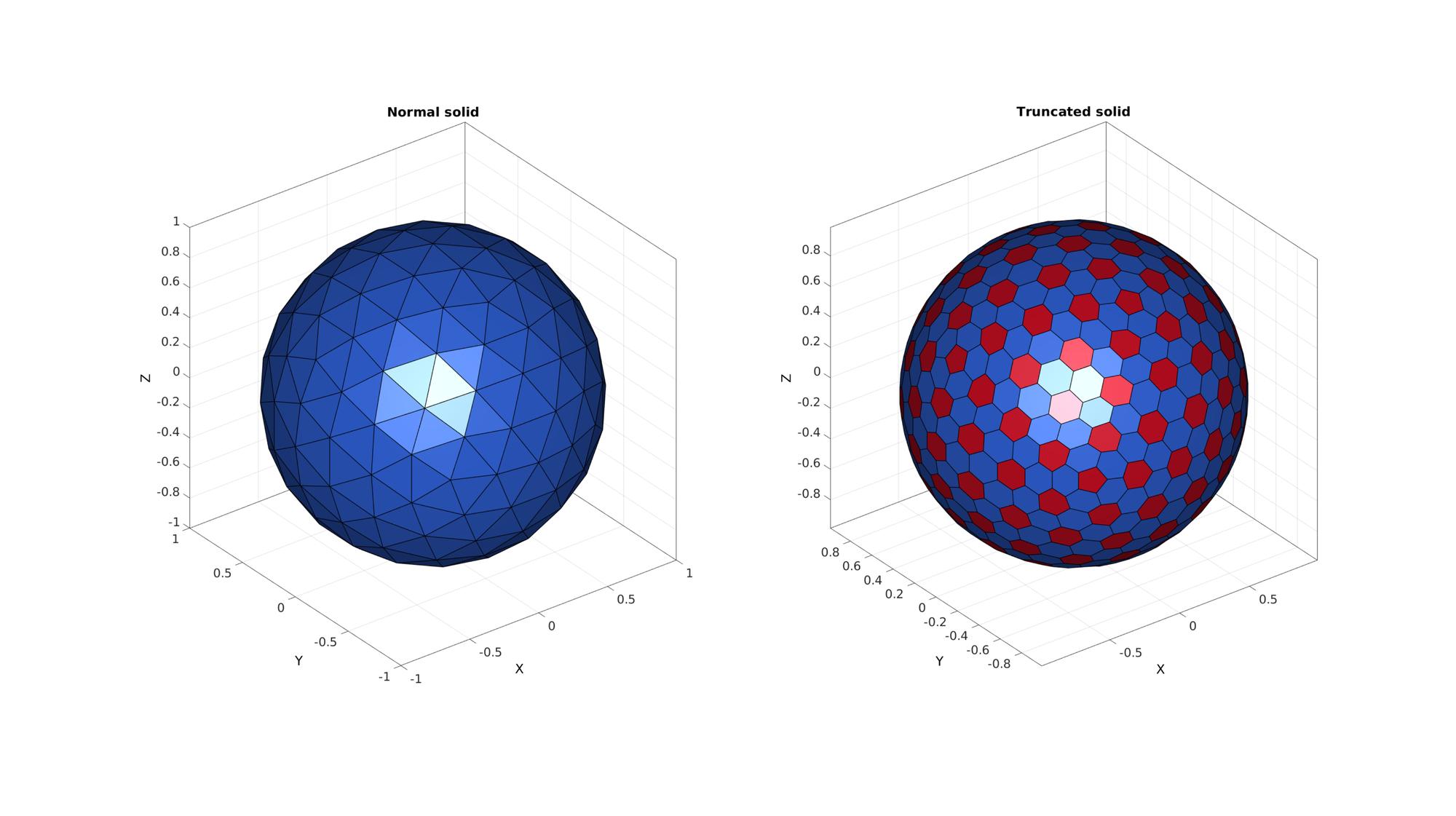
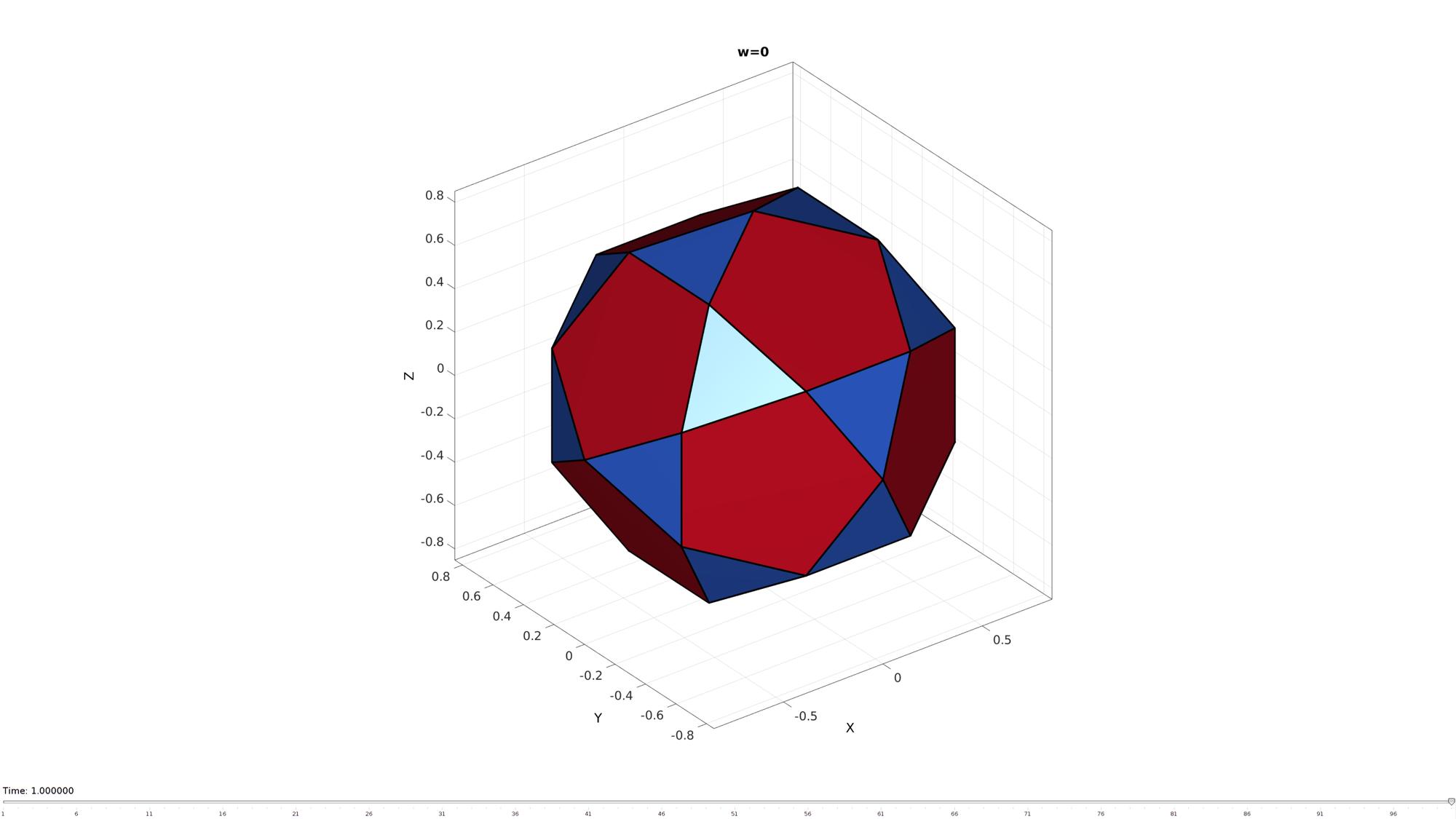
Create animated view to study effect of the truncation factor

Prepare visualization

[V,F]=platonic_solid(4,1);
w=tan(pi/(size(F,2)*2))/tan(pi/(size(F,2)));
[FC,VC,CC]=truncatePolyhedra(F,V,w);

hf=cFigure; hold on;
ht=title(['w=',num2str(w)]);
hp=gpatch(FC,VC,CC,'k',1,3);
axisGeom;
colormap(gjet(size(F,1)+size(V,1))); %icolorbar;
camlight headlight;
drawnow;

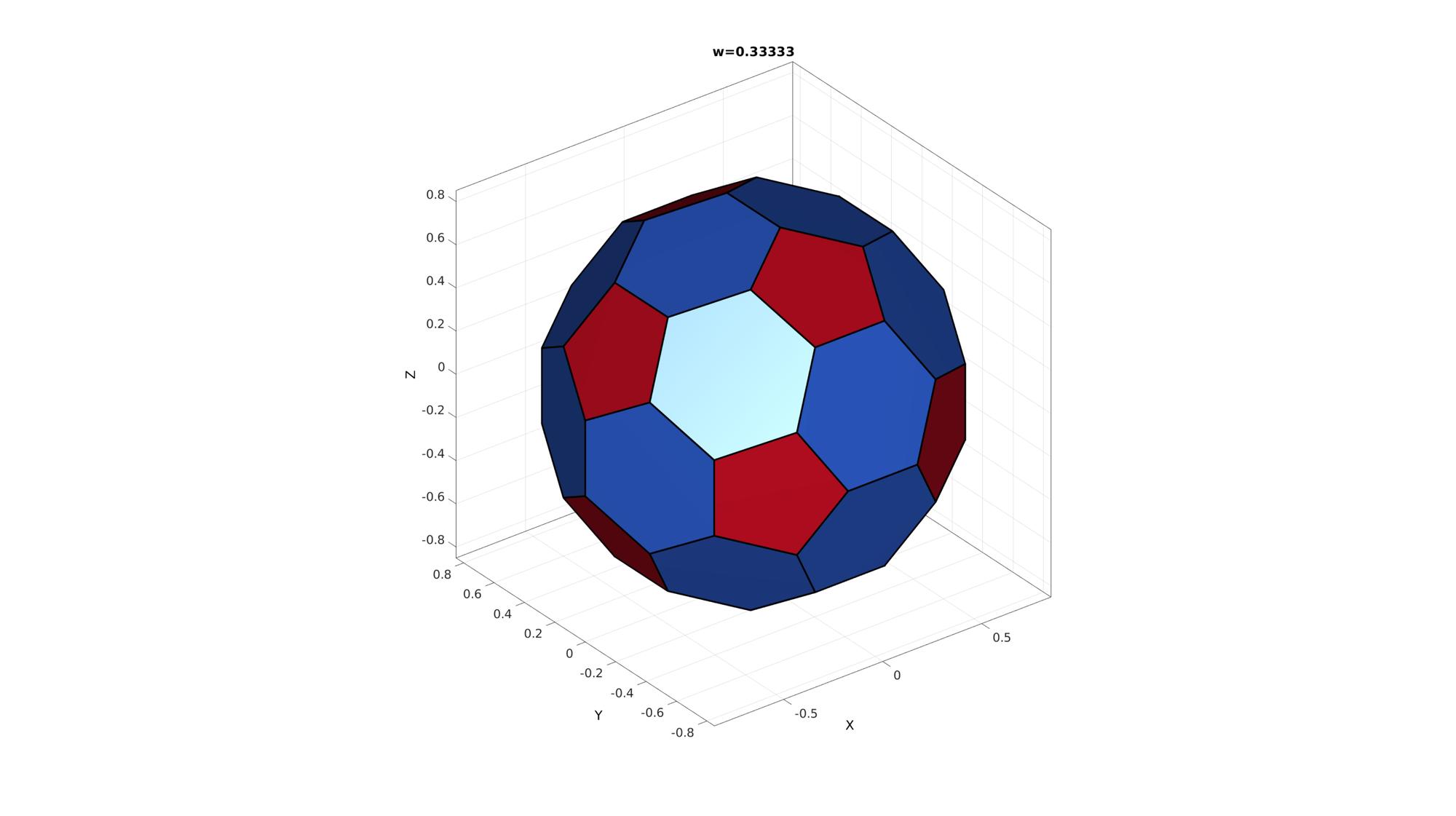
Create animation window

nSteps=100; %Number of animation steps

%Create the time vector
animStruct.Time=linspace(0,1,nSteps);

%Create w range
w=linspace(1,0,nSteps);

for q=1:1:nSteps
    [~,VC,~]=truncatePolyhedra(F,V,w(q));

    %Set entries in animation structure
    animStruct.Handles{q}=[hp]; %Handles of objects to animate
    for qh=1:1:numel(hp)
        animStruct.Props{q}(qh)={'Vertices'}; %Properties of objects to animate
        animStruct.Set{q}(qh)={VC}; %Property values for to set in order to animate
    end
    animStruct.Handles{q}(end+1)=[ht]; %Handles of objects to animate
    animStruct.Props{q}(end+1)={'String'}; %Properties of objects to animate
    animStruct.Set{q}(end+1)={['w=',num2str(w(q))]}; %Property values for to set in order to animate
end

anim8(hf,animStruct);

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2019 Kevin Mattheus Moerman

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2019a