triSurfSetDist

Below is a demonstration of the features of the triSurfSetDist function

Contents

clear; close all; clc;

PLOT SETTINGS

font_size=10;
cmap=gray(250);
falpha=1;
faceAlpha1=0.5;

Building test surfaces

%Defining shape 1 as a sphere
[F1,V1,~]=geoSphere(2,1);

%Defining shape 2 as a deformed sphere
[F2,V2,Vs]=geoSphere(3,1);
freqDef=3;
ampDef=0.25;
ampDefDiff=0.25;
n1=Vs(:,3)+(ampDef-ampDefDiff)+ampDef*sin(freqDef*Vs(:,1));
[V2(:,1),V2(:,2),~]=sph2cart(Vs(:,1),Vs(:,2),n1);

Plotting surfaces

cFigure; hold on;
title('The two surfaces','FontSize',font_size);
gpatch(F1,V1,'g','k',faceAlpha1);
gpatch(F2,V2,'b','k',faceAlpha1);
axisGeom(gca,font_size);
camlight headlight;
drawnow;

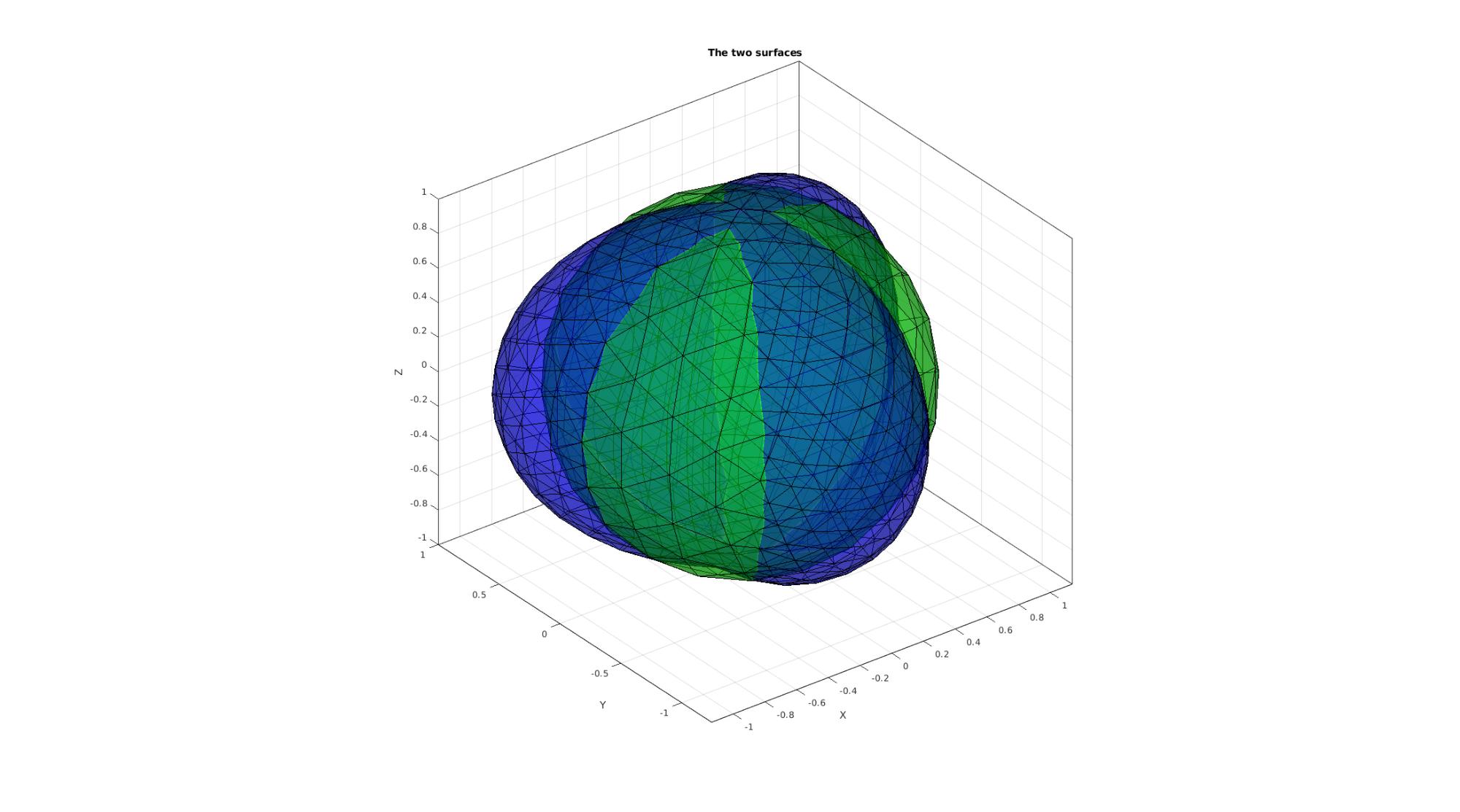
CLOSEST POINT BASED DISTANCE METRIC

[D2]=triSurfSetDist(F2,V2,F1,V1,'dist');

The above is equivalent to: D2=minDist(V2,V1);

Plotting results

cFigure; hold on;
title('Closest point distance metric on surface 2','FontSize',font_size);
gpatch(F1,V1,'w','none',faceAlpha1);
hp=gpatch(F2,V2,D2,'k'); hp.FaceColor='Interp';
colormap gjet; colorbar;
axisGeom(gca,font_size);
camlight headlight;
drawnow;

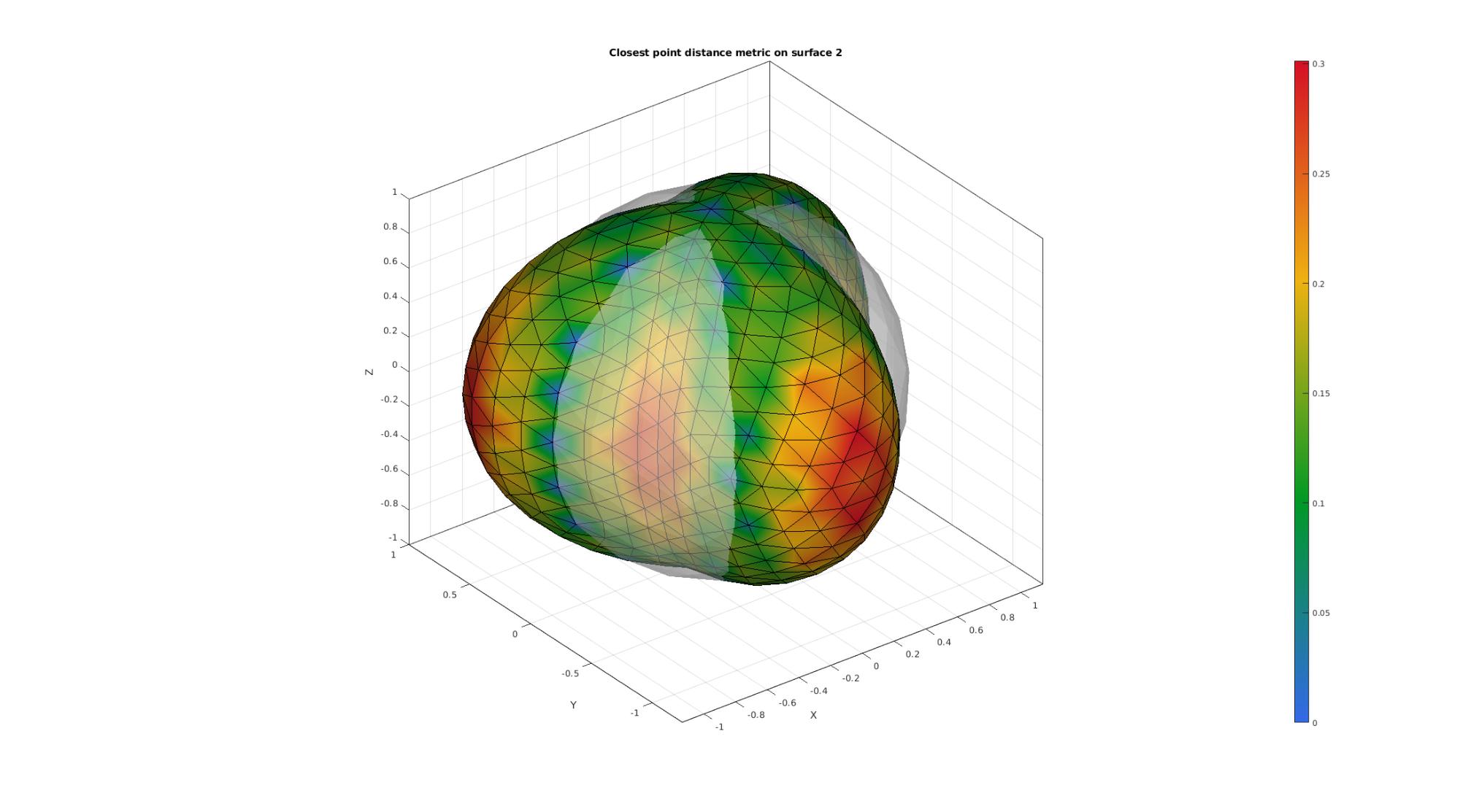
RAY TRACING DISTANCE METRIC

[D2]=triSurfSetDist(F2,V2,F1,V1,'ray');

Plotting results

cFigure; hold on;
title('Closest point distance metric on surface 2','FontSize',font_size);
gpatch(F1,V1,'w','none',faceAlpha1);
hp=gpatch(F2,V2,D2,'k'); hp.FaceColor='Interp';
colormap gjet; colorbar;
axisGeom(gca,font_size);
camlight headlight;
drawnow;

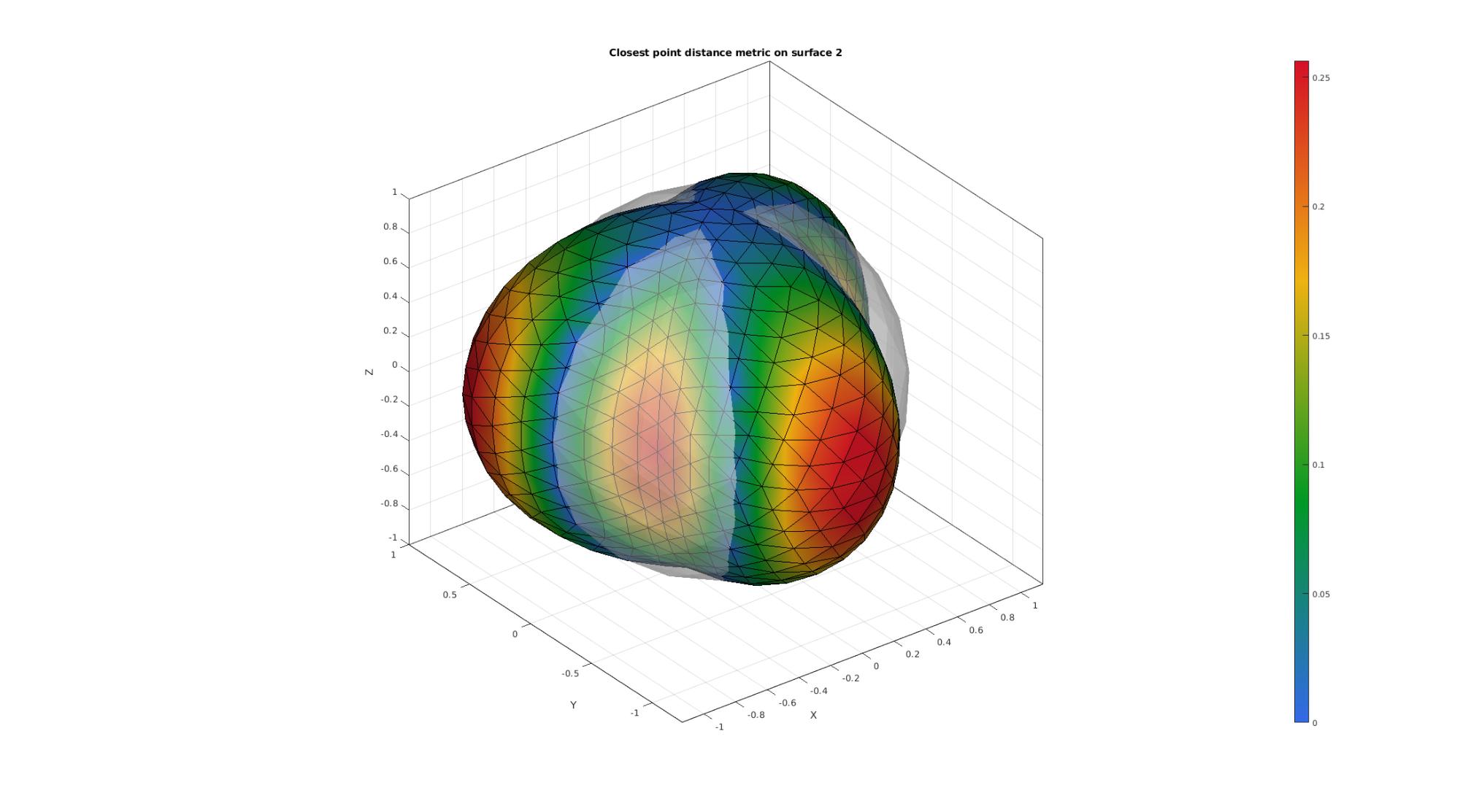
NOTE ON RAY TRACING DISTANCE METRIC AND NORMAL DIRECTIONS THAT DO NOT INTERSECT

The 'dist' method always finds a closest distance result for all points of the surface. However for the ray method the surface normals do not always trace to the other surface. The below example illustrates this. The curvature of the top and bottom regions means the normal direction rays do not intersect with the surface 1.

%Stretching shape in Z-direction
V2(:,3)=V2(:,3)*2;

%Compute distance metric
[D2]=triSurfSetDist(F2,V2,F1,V1,'ray');

Plotting results

cFigure; hold on;
title('Closest point distance metric on surface 2','FontSize',font_size);
gpatch(F1,V1,'w','none',faceAlpha1);
hp=gpatch(F2,V2,D2,'k'); hp.FaceColor='Interp';
colormap gjet; colorbar;
axisGeom(gca,font_size);
camlight headlight;
drawnow;

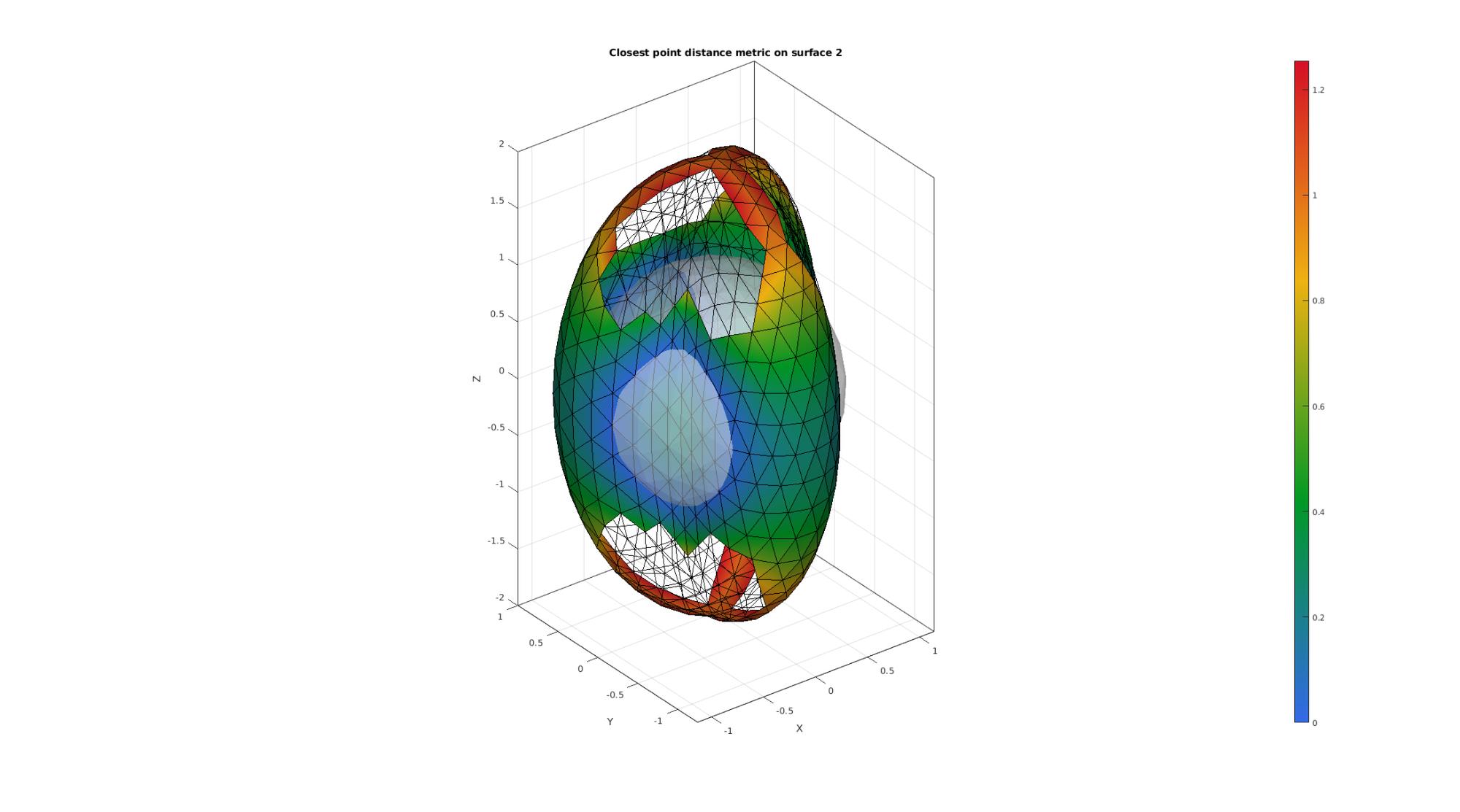
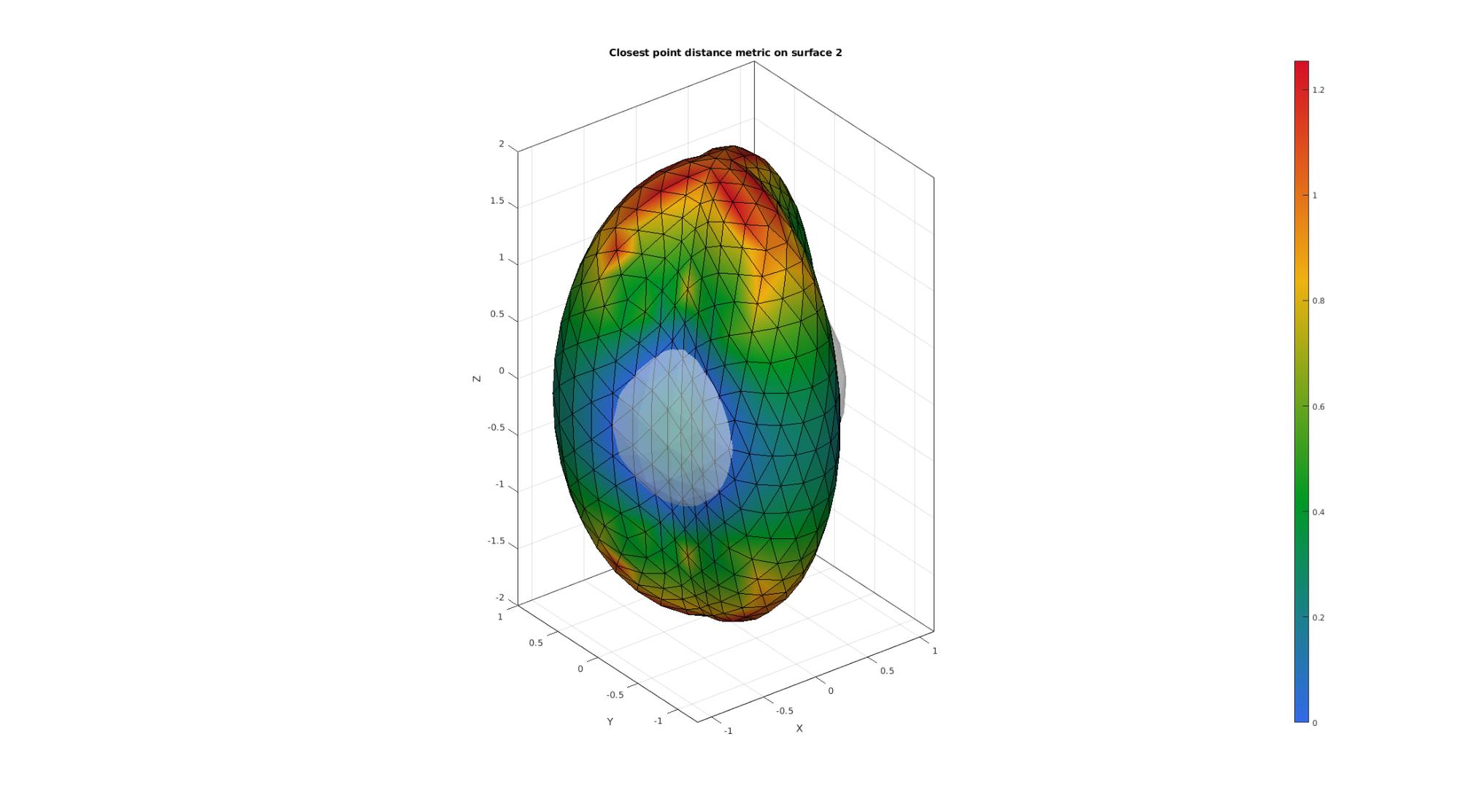
EXAMPLE TO FIX NAN's

%Logic for NaN's
L=isnan(D2);

%Use dist method where NaN occured
[D2_nan]=triSurfSetDist(F2,V2(L,:),F1,V1,'dist');
D2(L)=D2_nan;

Plotting results

cFigure; hold on;
title('Closest point distance metric on surface 2','FontSize',font_size);
gpatch(F1,V1,'w','none',faceAlpha1);
hp=gpatch(F2,V2,D2,'k'); hp.FaceColor='Interp';
colormap gjet; colorbar;
axisGeom(gca,font_size);
camlight headlight;
drawnow;

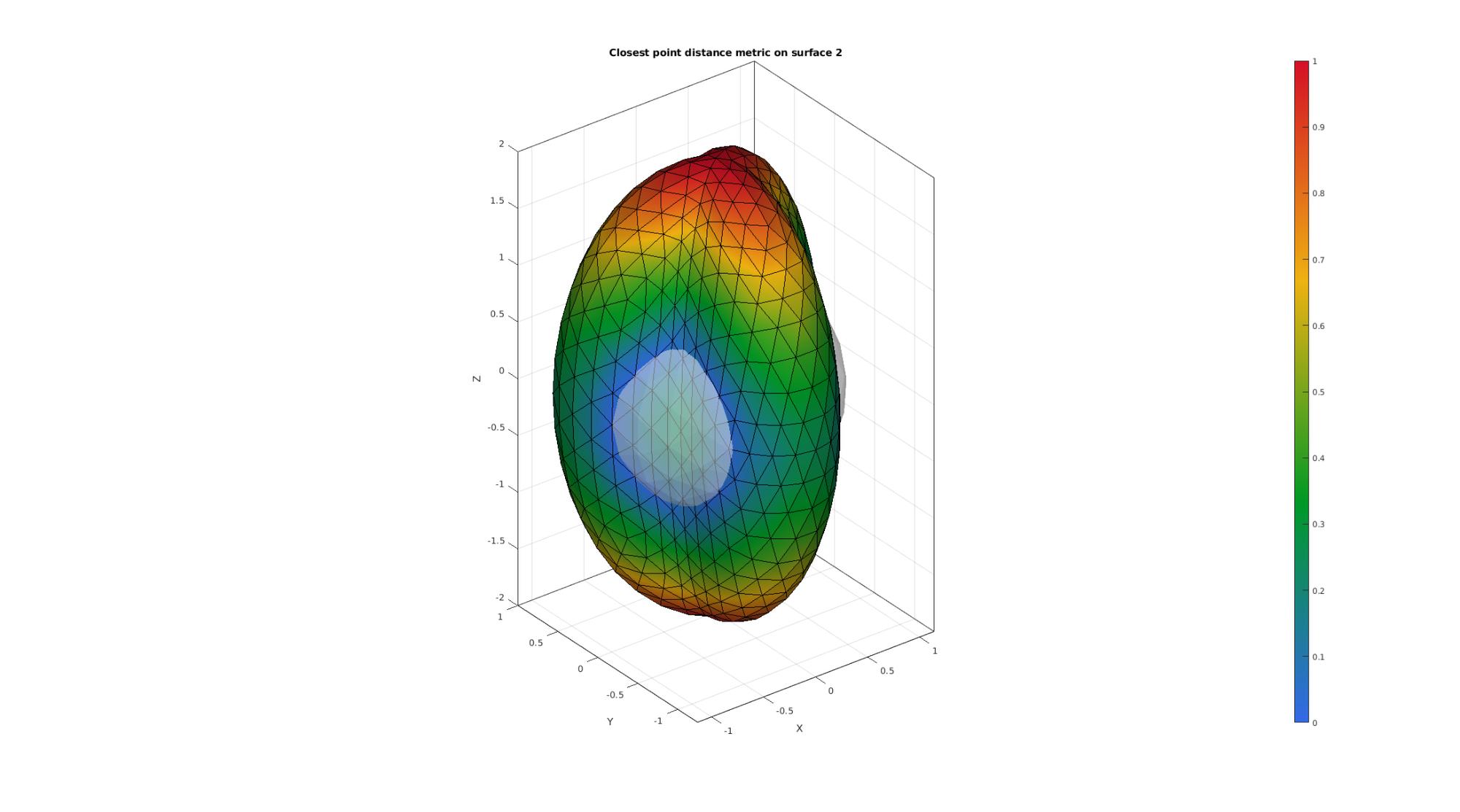
EXAMPLE OF "HYBRID APPROACH"

A hybrid approach is also possible whereby the output is the smallest distance for the two methods.

%Compute distance metric
[D2]=triSurfSetDist(F2,V2,F1,V1,'dist-ray');

Plotting results

cFigure; hold on;
title('Closest point distance metric on surface 2','FontSize',font_size);
gpatch(F1,V1,'w','none',faceAlpha1);
hp=gpatch(F2,V2,D2,'k'); hp.FaceColor='Interp';
colormap gjet; colorbar;
axisGeom(gca,font_size);
camlight headlight;
drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2006-2021 Kevin Mattheus Moerman and the GIBBON contributors

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2021a