HELP_euler2DCM

Below is a demonstration of the features of the euler2DCM function

Syntax
Description
Examples
Setting up rotation matrices based on angles.
Creating multiple rotation matrices
Using symbolic angles

clear; close all; clc;

Syntax

[Q]=euler2DCM(a);

Description

This function uses the input Euler angle set a, a 1x3 vector, to compute a rotation tensor Q, also known as a direction cosine matrix (DCM). See also DCM2euler

Examples

Plot settings

fontSize=25;

Setting up rotation matrices based on angles.

Get example patch data

[F,V]=parasaurolophus;

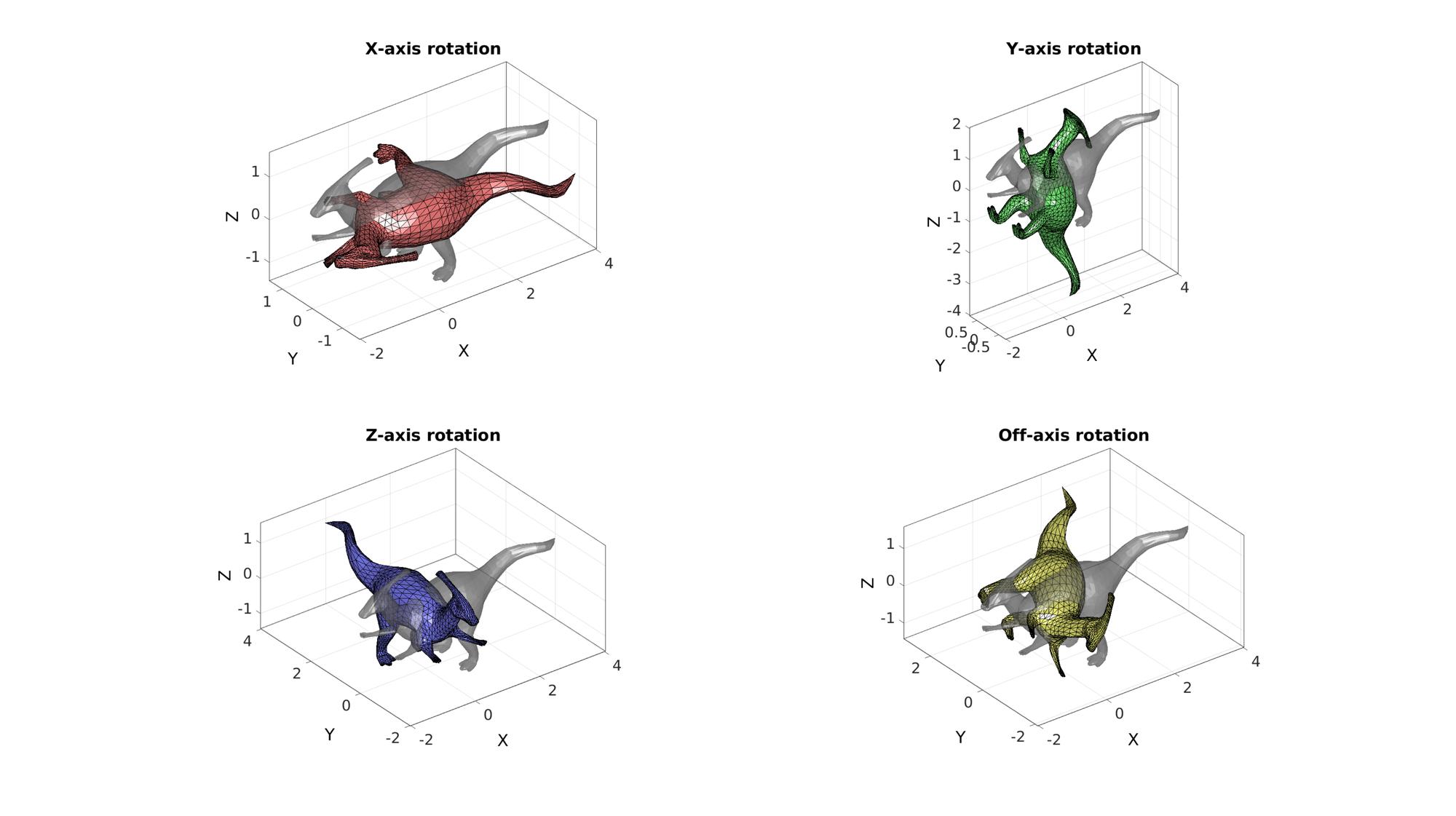
Defining sets of Euler angles for X, Y and Z axis rotation

E1=[0.5*pi 0 0]; %Just x
E2=[0 0.5*pi 0]; %Just y
E3=[0 0 0.5*pi]; %Just z
E4=[0.25*pi 0.25*pi 0.25*pi]; %All

Use euler2DCM function to define the rotation matrices

[R1]=euler2DCM(E1);
[R2]=euler2DCM(E2);
[R3]=euler2DCM(E3);
[R4]=euler2DCM(E4);

Rotate the coordinates. One may define the rotation in the form V*R or (R*V')' depending if pre-, or post-rotation is applied, whereby V*R=(R'*V')'.

V1=(R1*V')';
V2=(R2*V')';
V3=(R3*V')';
V4=(R4*V')';

Plotting data

hf=cFigure;

subplot(2,2,1);
title('X-axis rotation','FontSize',fontSize);
gpatch(F,V,'kw','none',0.5);
gpatch(F,V1,'rw');
axisGeom(gca,fontSize);
camlight headlight;

subplot(2,2,2);
title('Y-axis rotation','FontSize',fontSize);
gpatch(F,V,'kw','none',0.5);
gpatch(F,V2,'gw');
axisGeom(gca,fontSize);
camlight headlight;

subplot(2,2,3);
title('Z-axis rotation','FontSize',fontSize);
gpatch(F,V,'kw','none',0.5);
gpatch(F,V3,'bw');
axisGeom(gca,fontSize);
camlight headlight;

subplot(2,2,4);
title('Off-axis rotation','FontSize',fontSize);
gpatch(F,V,'kw','none',0.5);
gpatch(F,V4,'yw');
axisGeom(gca,fontSize);
camlight headlight;

drawnow;

A second output can also be requested which is the inverse rotation matrix.

[Q,Qi]=euler2DCM([randn(1,3)*pi]);
Q
Qi

Q =

    0.8566   -0.3911   -0.3366
    0.3092    0.9113   -0.2720
    0.4131    0.1289    0.9015


Qi =

    0.8566    0.3092    0.4131
   -0.3911    0.9113    0.1289
   -0.3366   -0.2720    0.9015

i.e. such that the following :

Vr=(Q*V')'; %The rotated coordinates
Vn=(Qi*Vr')'; %The normal coordinates after transforming back the rotated coordinates using inverse matrix

Note that the sum of squared differences for instance is nearly zero

D=sum((V(:)-Vn(:)).^2)

D =

   8.5943e-29

Creating multiple rotation matrices

It is possible to define multiple rotation matrices at once by specifying a multi-row angle set

E=[0.25*pi 0 0; 0 0.5*pi 0]; %E.g. two angle sets are specified, 1 for each row

In this case the rotation matrices are stacked in the 3rd dimension

[Q]=euler2DCM(E)

Q(:,:,1) =

    1.0000         0         0
         0    0.7071   -0.7071
         0    0.7071    0.7071


Q(:,:,2) =

    0.0000         0    1.0000
         0    1.0000         0
   -1.0000         0    0.0000

Using symbolic angles

try
    syms a b c
    [Q1]=euler2DCM([a 0 0])
    [Q2]=euler2DCM([0 b 0])
    [Q3]=euler2DCM([0 0 c])
    [Q4]=euler2DCM([a b c])
catch
    warning('Symbolic toolbox likely missing')
end

 
Q1 =
 
[ 1,      0,       0]
[ 0, cos(a), -sin(a)]
[ 0, sin(a),  cos(a)]
 
 
Q2 =
 
[  cos(b), 0, sin(b)]
[       0, 1,      0]
[ -sin(b), 0, cos(b)]
 
 
Q3 =
 
[ cos(c), -sin(c), 0]
[ sin(c),  cos(c), 0]
[      0,       0, 1]
 
 
Q4 =
 
[                        cos(b)*cos(c),                       -cos(b)*sin(c),         sin(b)]
[ cos(a)*sin(c) + cos(c)*sin(a)*sin(b), cos(a)*cos(c) - sin(a)*sin(b)*sin(c), -cos(b)*sin(a)]
[ sin(a)*sin(c) - cos(a)*cos(c)*sin(b), cos(c)*sin(a) + cos(a)*sin(b)*sin(c),  cos(a)*cos(b)]

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.