constrainedDelaunayTetGen

Below is a demonstration of the features of the constrainedDelaunayTetGen function

Contents

Syntax

[TR]=constrainedDelaunayTetGen(V,C);

Description

The constrainedDelaunayTetGen function uses TetGen to create the constrained 3D Delaunay tesselation of point sets.

Examples

clear; close all; clc;

Plot settings

fontSize=15;
faceAlpha1=1;
faceAlpha2=0.5;
edgeColor=0.25*ones(1,3);
edgeWidth=1.5;
markerSize=25;

% path names
filePath=mfilename('fullpath');
savePath=fullfile(fileparts(filePath),'data','temp');

Creating example surface input data

% Defining a deformed and rotated torus shape
r=1; %Sphere radius
rc=2; %Central radius
nr=16;
nc=30;
ptype='tri';
[F,V]=patchTorus(r,nr,rc,nc,ptype);
[THETA,RHO] = cart2pol(V(:,1),V(:,2));
V(:,3)=V(:,3)+sin(3*THETA);
[R,~]=euler2DCM([0.5*pi 0.5*pi 0.*pi]);
V=V*R;

Plotting surface model

cFigure;
title('The surface model','FontSize',fontSize);
hold on;
gpatch(F,V,'gw','k');
camlight headlight;
axisGeom(gca,fontSize);
drawnow;

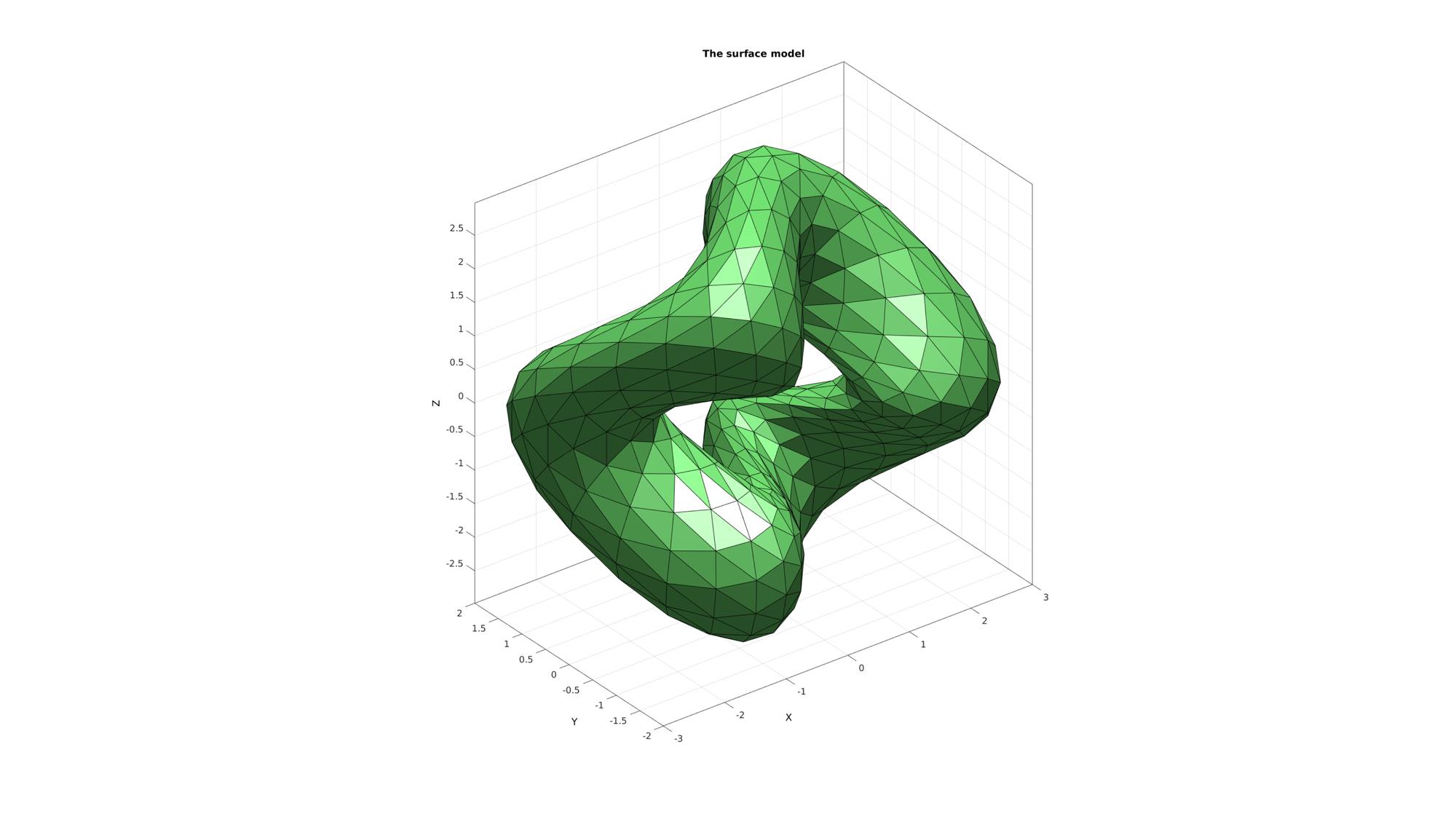
Example: Using MATLAB's delaunayTriangulation to compute the unconstrained 3D Delaunay tesselation

Computing the unconstrained 3D Delaunay tesselation of point set

[DT]=delaunayTriangulation(V);

%Access the produces tetrahedrons and vertices (possibly different from
%input vertices)
TET1=DT.ConnectivityList;
V1=DT.Points;
[F1]=element2patch(TET1,[],'tet4');

Example: Using TetGen based constrainedDelaunayTetGen to compute the unconstrained 3D Delaunay tesselation

Computing the constrained 3D Delaunay tesselation of point set (i.e. faces are matched)

C=[]; %i.e. no constraints
[TR]=constrainedDelaunayTetGen(V,C);
TET2=TR.ConnectivityList;
V2=TR.Points;
[F2]=element2patch(TET2,[],'tet4');

 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- TETGEN Tetrahedral meshing --- 20-Jun-2019 14:44:18
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- Writing NODE file --- 20-Jun-2019 14:44:18
--- Done --- 20-Jun-2019 14:44:18
--- Running TetGen to mesh input boundary--- 20-Jun-2019 14:44:18
Opening /mnt/data/MATLAB/GIBBON/data/temp/temp.node.
--- Done --- 20-Jun-2019 14:44:18
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- Importing TetGen files --- 20-Jun-2019 14:44:18
--- Done --- 20-Jun-2019 14:44:18

Plotting surface model

cFigure;

subplot(1,2,1);
title('The unconstrained MATLAB tesselation','FontSize',fontSize);
hold on;
gpatch(F1,V1,'rw','k');
camlight headlight;
axisGeom(gca,fontSize);

subplot(1,2,2);
title('The unconstrained TetGen tesselation','FontSize',fontSize);
hold on;
gpatch(F2,V2,'gw','k');
camlight headlight;
axisGeom(gca,fontSize);
drawnow;

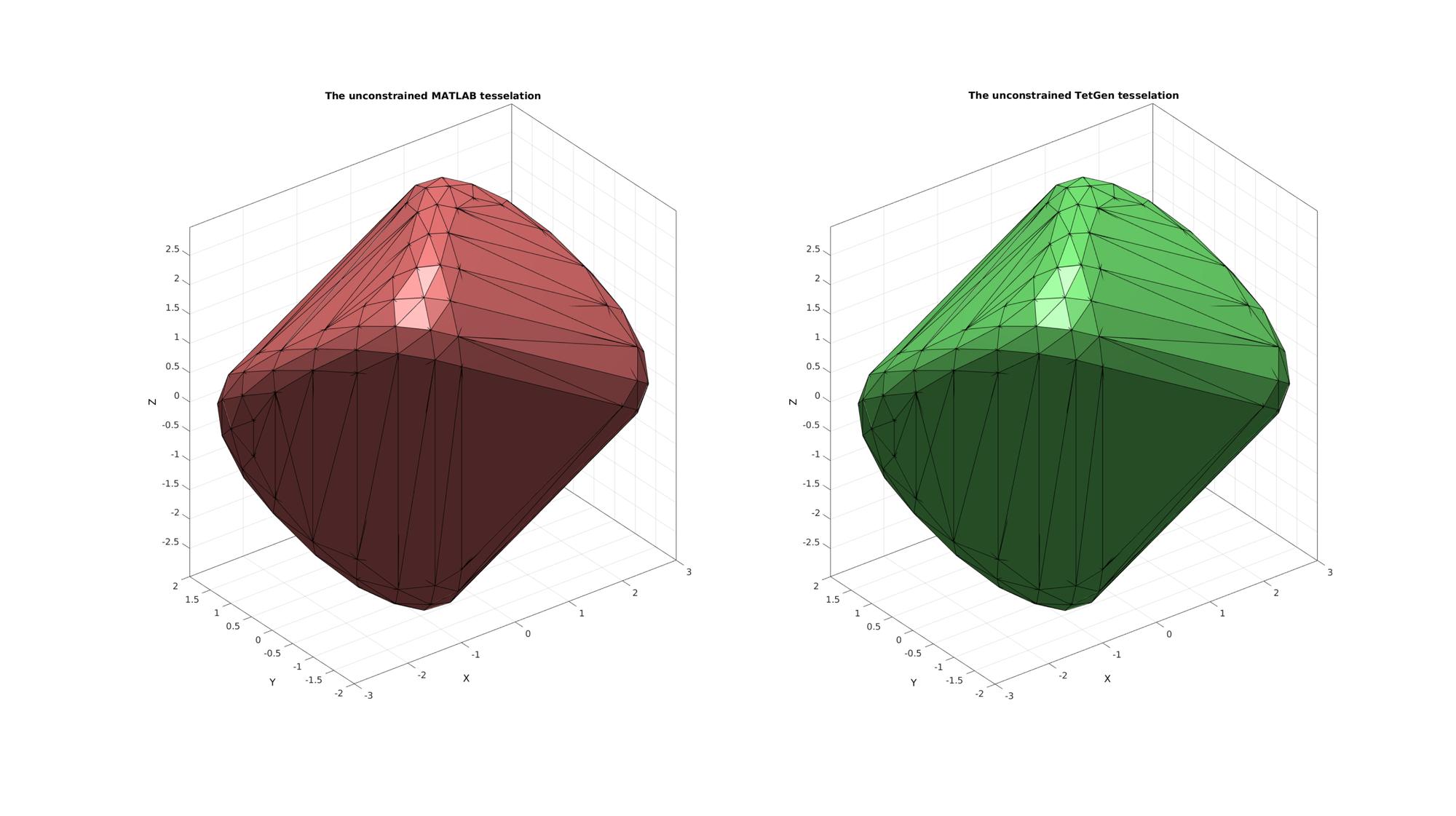
Example: Using TetGen based constrainedDelaunayTetGen to compute the constrained 3D Delaunay tesselation

Computing the constrained 3D Delaunay tesselation of point set (i.e. faces are matched)

C=F; %i.e. The faces form the constraints
[TR]=constrainedDelaunayTetGen(V,C);
TET2=TR.ConnectivityList;
V2=TR.Points;
[F2]=element2patch(TET2,[],'tet4');

 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- TETGEN Tetrahedral meshing --- 20-Jun-2019 14:44:20
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- Writing SMESH file --- 20-Jun-2019 14:44:20
----> Adding node field
----> Adding facet field
----> Adding holes specification
----> Adding region specification
--- Done --- 20-Jun-2019 14:44:20
--- Running TetGen to mesh input boundary--- 20-Jun-2019 14:44:20
Opening /mnt/data/MATLAB/GIBBON/data/temp/temp.smesh.
--- Done --- 20-Jun-2019 14:44:20
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- Importing TetGen files --- 20-Jun-2019 14:44:20
--- Done --- 20-Jun-2019 14:44:20

Plotting surface model

cFigure;

subplot(1,2,1);
title('The unconstrained tesselation (convex hull)','FontSize',fontSize);
hold on;
gpatch(F1,V1,'rw','k');
camlight headlight;
axisGeom(gca,fontSize);

subplot(1,2,2);
title('The constrained TetGen tesselation','FontSize',fontSize);
hold on;
gpatch(F2,V2,'gw','k');
camlight headlight;
axisGeom(gca,fontSize);
drawnow;

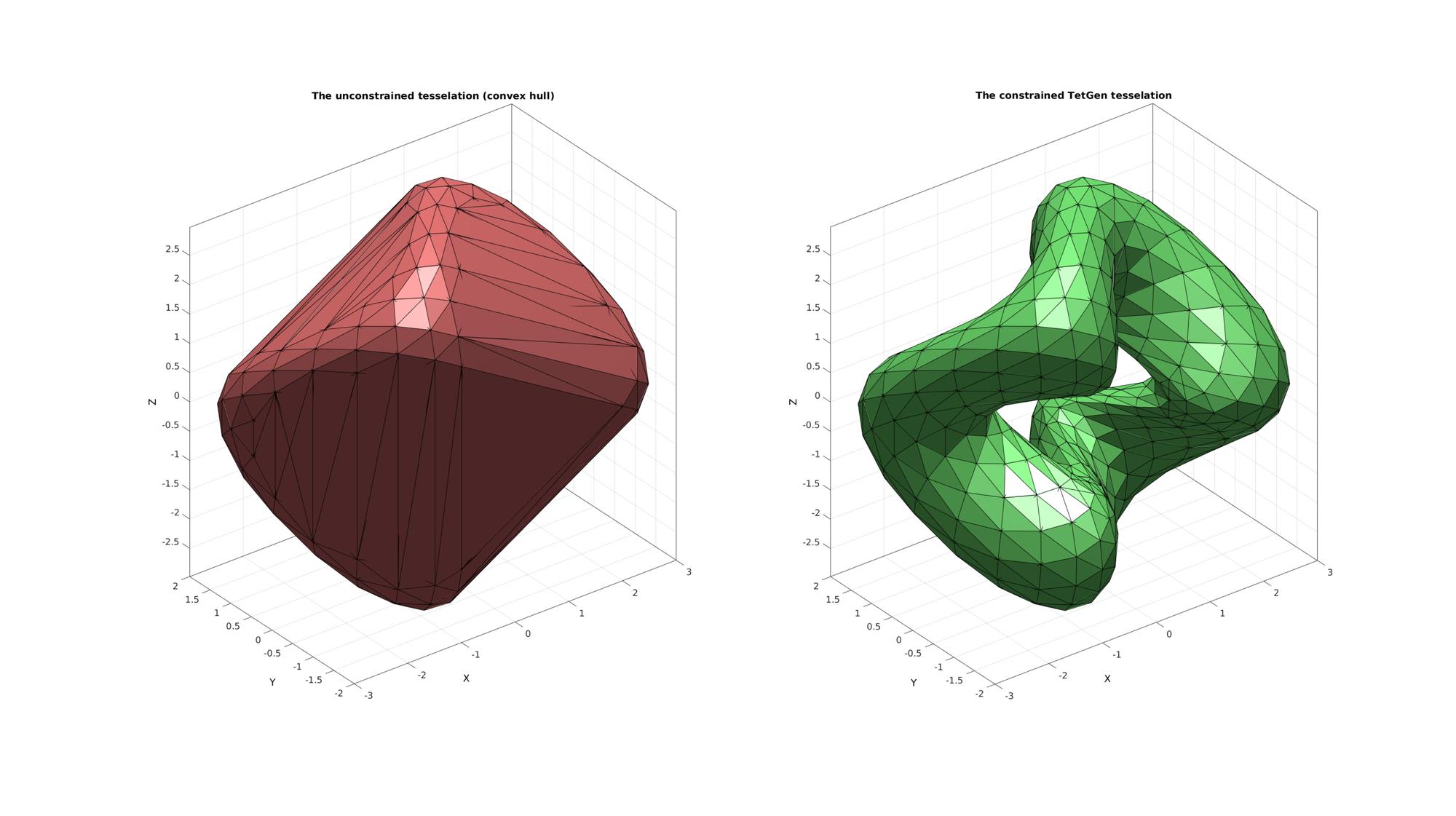
Example: Computing constrained 3D Delaunay tesselations with interior points

First the triSurf2Im function is used to mesh the interior

[edgeLengths]=patchEdgeLengths(F,V);
edgeLengthsMean=mean(edgeLengths);

voxelSize=edgeLengthsMean/2; % The output image voxel size.

% Using |triSurf2Im| function to convert patch data to image data
[M,G,bwLabels]=triSurf2Im(F,V,voxelSize);
imOrigin=G.origin;

Visualize interor voxels

cFigure;
subplot(1,2,1);
title('Closed triangulated surface','FontSize',fontSize);
hold on;
gpatch(F,V,'g','k',faceAlpha1);
camlight('headlight');
axisGeom(gca,fontSize);

subplot(1,2,2);
title('Boundary, intertior and exterior image','FontSize',fontSize);
hold on;

gpatch(F,V,'g','none',faceAlpha2);

L_plot=false(size(M));
L_plot(:,:,round(size(M,3)/2))=1;
[Fm,Vm,Cm]=ind2patch(L_plot,double(M),'sk');
[Vm(:,1),Vm(:,2),Vm(:,3)]=im2cart(Vm(:,2),Vm(:,1),Vm(:,3),voxelSize*ones(1,3));
Vm=Vm+imOrigin(ones(size(Vm,1),1),:);
gpatch(Fm,Vm,Cm,'k',faceAlpha1);

L_plot=false(size(M));L_plot(round(size(M,1)/2),:,:)=1;
[Fm,Vm,Cm]=ind2patch(L_plot,M,'si');
[Vm(:,1),Vm(:,2),Vm(:,3)]=im2cart(Vm(:,2),Vm(:,1),Vm(:,3),voxelSize*ones(1,3));
Vm=Vm+imOrigin(ones(size(Vm,1),1),:);
gpatch(Fm,Vm,Cm,'k',faceAlpha1);

L_plot=false(size(M));L_plot(:,round(size(M,2)/2),:)=1;
[Fm,Vm,Cm]=ind2patch(L_plot,M,'sj');
[Vm(:,1),Vm(:,2),Vm(:,3)]=im2cart(Vm(:,2),Vm(:,1),Vm(:,3),voxelSize*ones(1,3));
Vm=Vm+imOrigin(ones(size(Vm,1),1),:);
gpatch(Fm,Vm,Cm,'k',faceAlpha1);

colormap(gray(3)); caxis([0 2]);
hc=colorbar;
set(hc,'YTick',[1/3 1 5/3]);
set(hc,'YTickLabel',{'Exterior','Boundary','Intertior'});
camlight('headlight');
axisGeom(gca,fontSize);
drawnow;

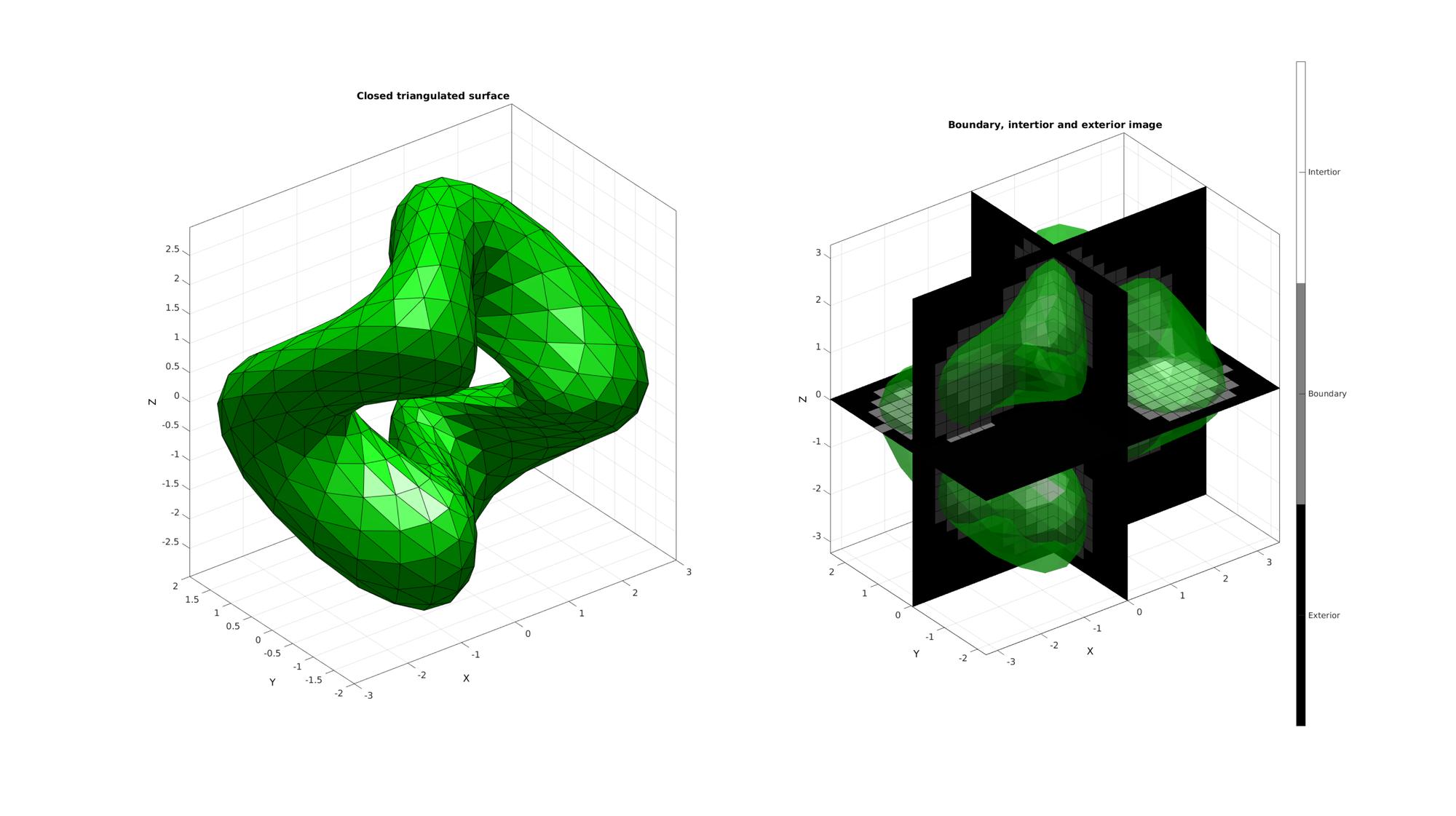
Convert interior voxels to interior points

indInterior=find(M==2);
[I,J,K]=ind2sub(size(M),indInterior);
[X,Y,Z]=im2cart(I,J,K,voxelSize*ones(1,3));
Vi=[X(:) Y(:) Z(:)];
Vi=Vi+imOrigin(ones(size(Vi,1),1),:);

Plotting surface model and interior points

cFigure;
title('Visualizing a mesh of interior points','FontSize',fontSize);
hold on;
gpatch(F,V,'kw','none',0.1);
plotV(Vi,'k.','MarkerSize',markerSize);
camlight('headlight');
axisGeom(gca,fontSize);
drawnow;

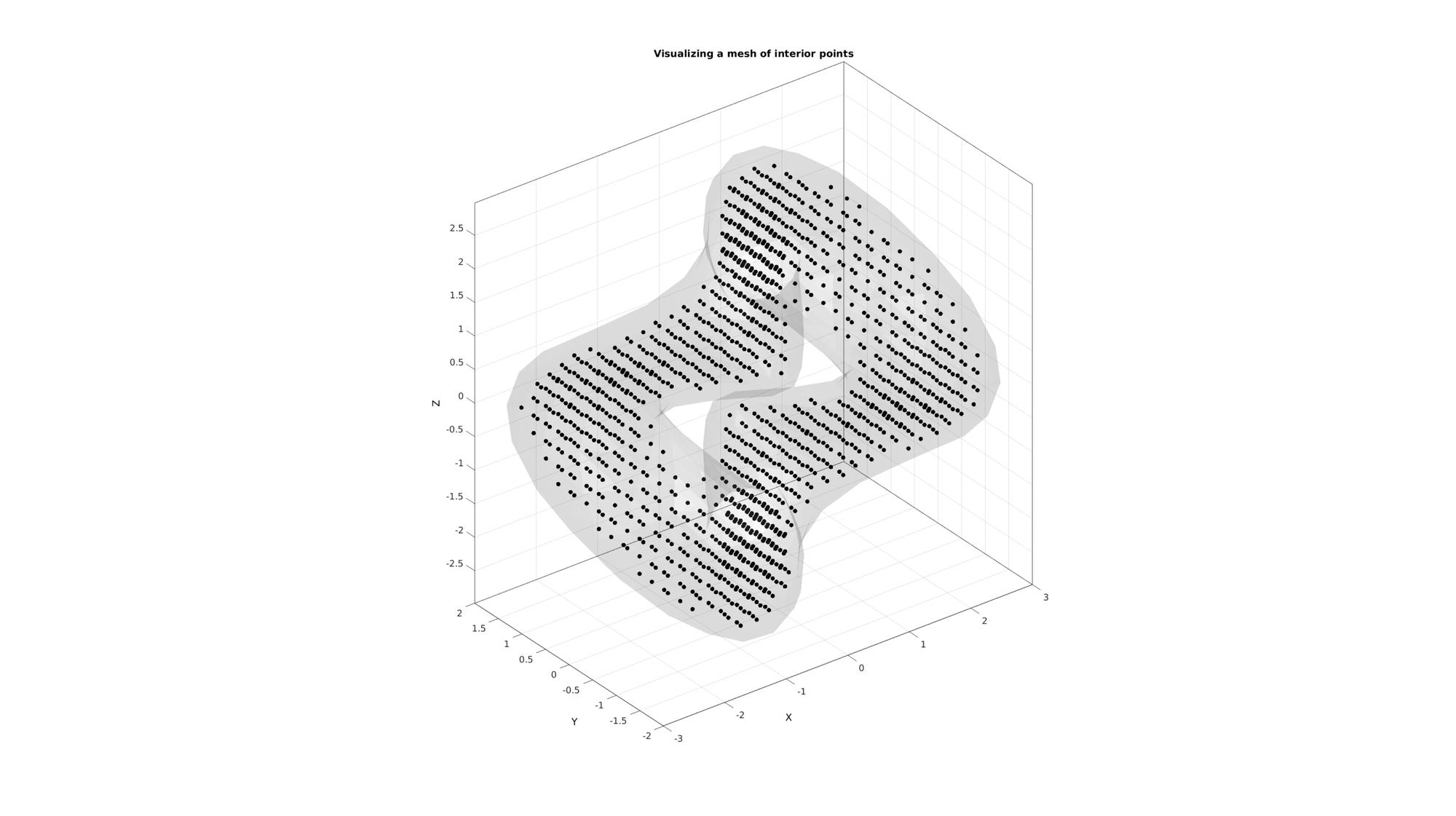
Compute constrained Delaunay tesselation

C=F; %i.e. the faces form the constraints
Vt=[V;Vi]; %The face vertices and interior vertices combined
[TR]=constrainedDelaunayTetGen(Vt,C);
TET3=TR.ConnectivityList;
V3=TR.Points;
[F3]=element2patch(TET3,[],'tet4');

%Create data for cut view
X=V3(:,3); XE=mean(X(TET3),2);
L=XE<mean(X(:));
[F3c]=element2patch(TET3(L,:),[],'tet4');

 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- TETGEN Tetrahedral meshing --- 20-Jun-2019 14:44:24
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- Writing SMESH file --- 20-Jun-2019 14:44:24
----> Adding node field
----> Adding facet field
----> Adding holes specification
----> Adding region specification
--- Done --- 20-Jun-2019 14:44:24
--- Running TetGen to mesh input boundary--- 20-Jun-2019 14:44:24
Opening /mnt/data/MATLAB/GIBBON/data/temp/temp.smesh.
--- Done --- 20-Jun-2019 14:44:24
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
--- Importing TetGen files --- 20-Jun-2019 14:44:24
--- Done --- 20-Jun-2019 14:44:24

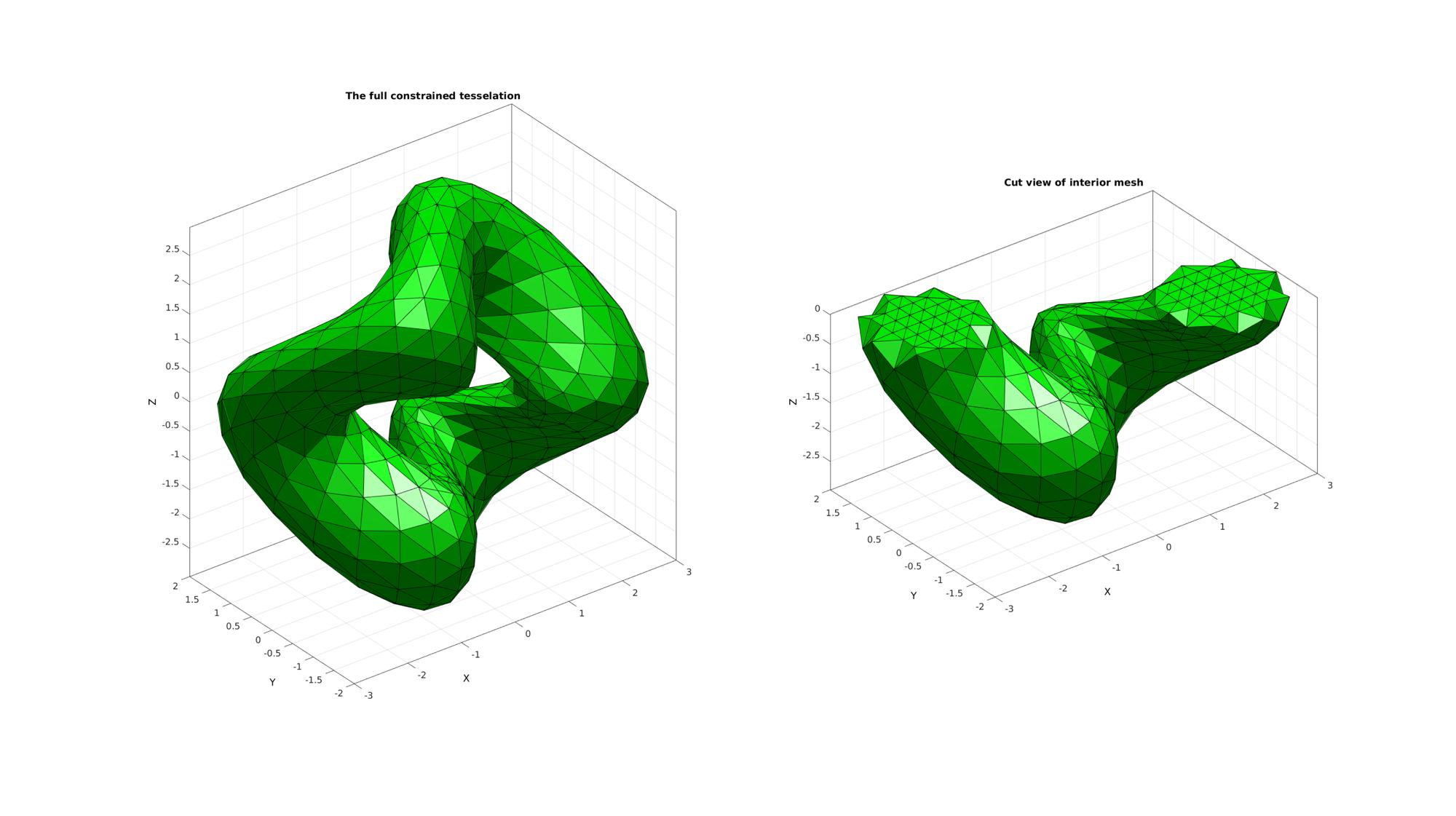
Plotting meshed model

cFigure;
subplot(1,2,1);
title('The full constrained tesselation','FontSize',fontSize);
hold on;
gpatch(F3,V3,'g','k',faceAlpha1);
camlight('headlight');
axisGeom(gca,fontSize);

subplot(1,2,2);
title('Cut view of interior mesh','FontSize',fontSize);
hold on;
gpatch(F3c,V3,'g','k',faceAlpha1);
camlight('headlight');
axisGeom(gca,fontSize);
drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2019 Kevin Mattheus Moerman

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2019a