axisLim

Below is a demonstration of the features of the axisLim function

Contents

clear; close all; clc;

Syntax

axLim=axisLim(V);

Description

This function computes appropiate axis limits for the input vertices V. The vertices may be an k x l x m array, where by by k is the number of vertices, l is the number of dimensions (e.g. 2 or 3), and m is for instance a time (or other) dimension. The function returs axLim which are appropriate axis limits such that the coordinates in V can be displayed appropriately (and in a tight fashion).

Examples

Example 1: setting axis limits tightly around a coordinate set in 2D

Create example data

t=linspace(0,2*pi,250)';
r=5+2*sin(5*t);
V=r.*[cos(t) sin(t)];

Compute appropriate limits

axLim=axisLim(V) %Axis limits for vertices

axLim =

   -6.6976    6.7000   -5.8390    6.9989

Assign axis limits using axisLim

cFigure;
plot(V(:,1),V(:,2),'b-');
axis equal; axis(axisLim(V));
drawnow;

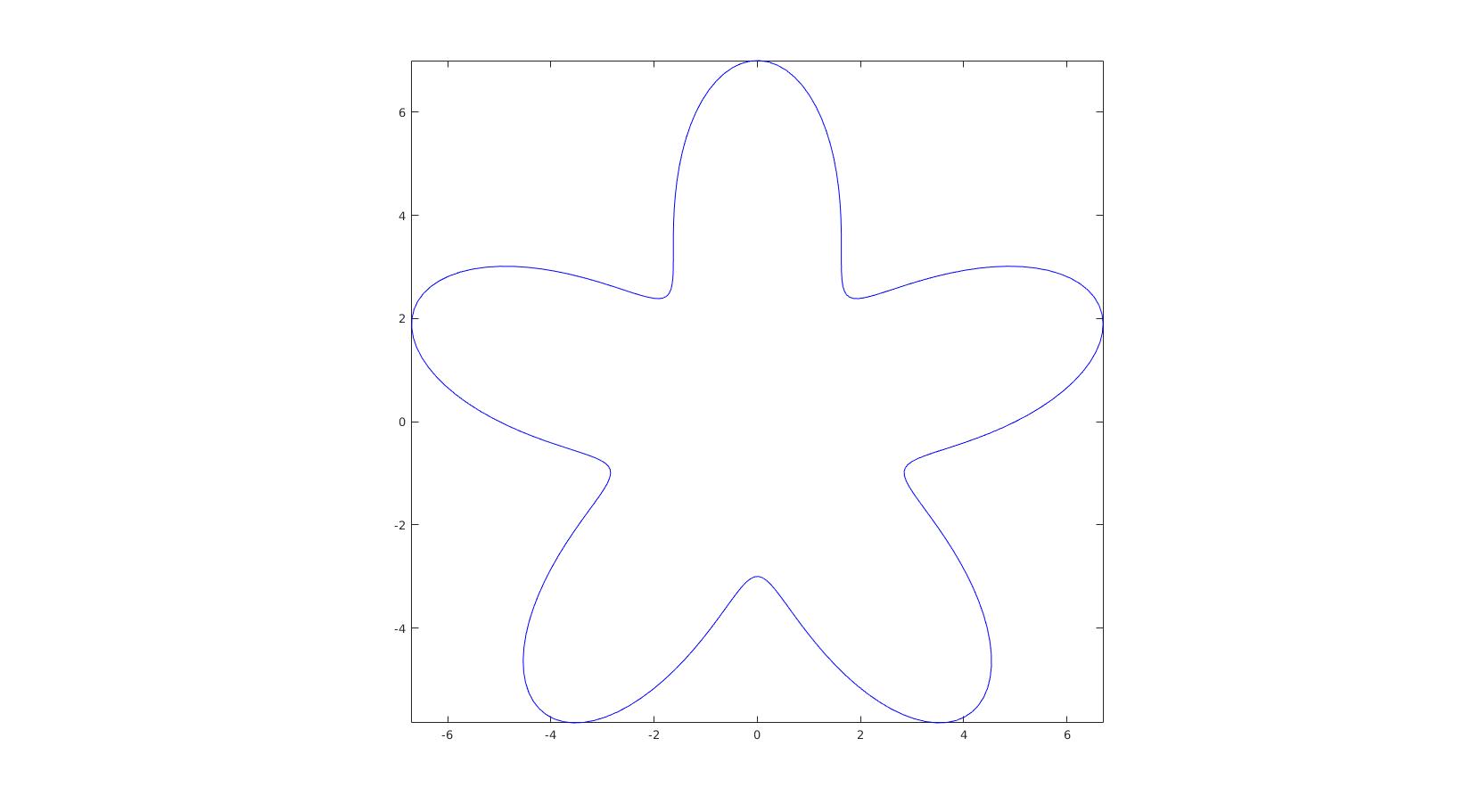
Example 2: setting axis limits tightly around a coordinate set in 3D

Create example data

[F,V]=stanford_bunny;

Compute appropriate limits

axLim=axisLim(V) %Axis limits for vertices

axLim =

  -77.1042   77.6348  -59.4666   60.6226  -77.2629   76.0109

Assign axis limits using axisLim

cFigure;
gpatch(F,V);
axisGeom; camlight headlight;
axis(axisLim(V));
gdrawnow;

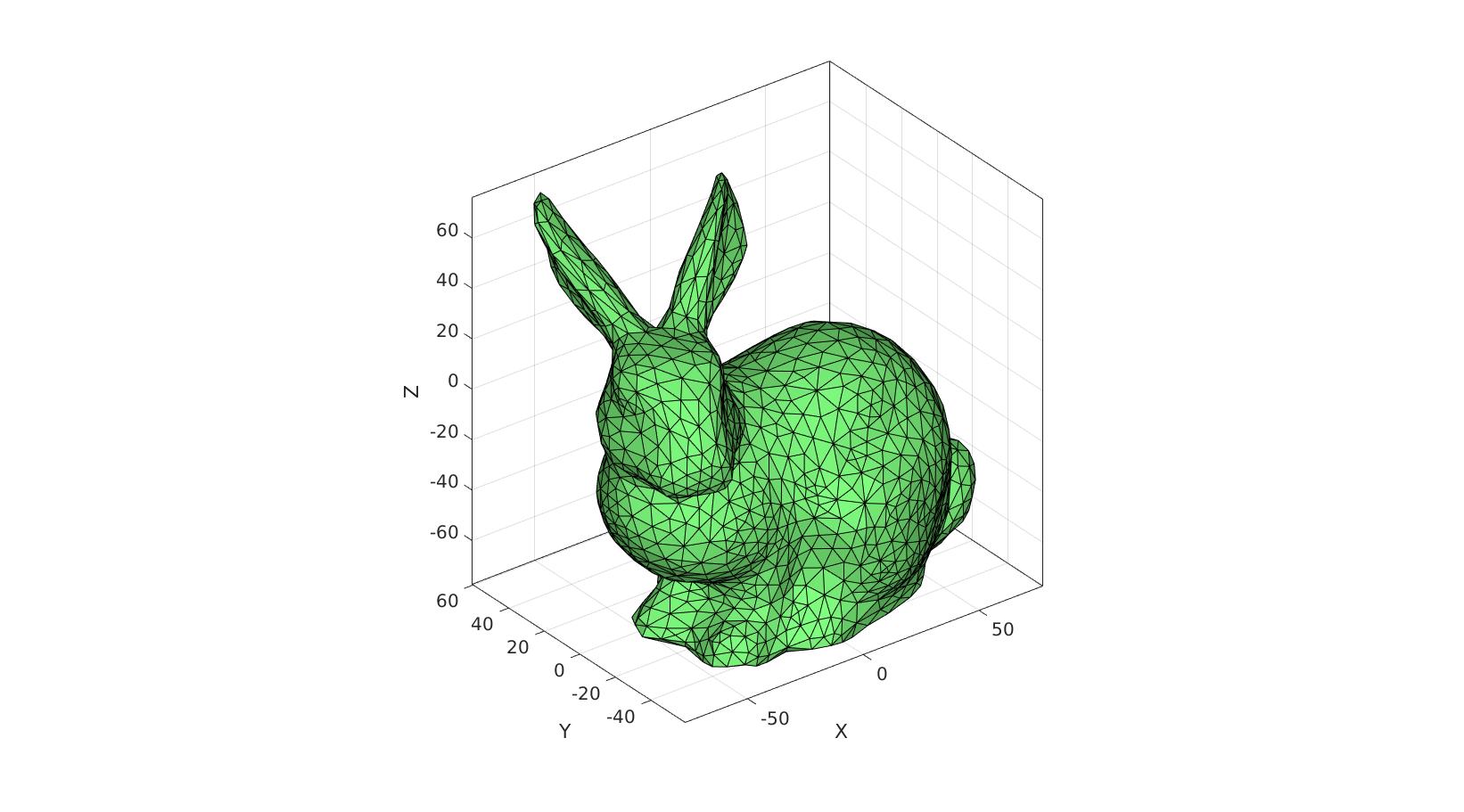
Example 3: setting axis limits tightly around multiple coordinate sets in 3D

Create example data

[F1,V1]=graphicsModels(3);
[F2,V2]=graphicsModels(4);
V2=V2+1;

Compute appropriate limits

axLim=axisLim(V1,V2) %Axis limits for vertices

axLim =

   -1.0247    5.0281   -0.3258    1.8240   -0.6125    2.5817

Assign axis limits using axisLim

cFigure; hold on;
gpatch(F1,V1,'gw');
gpatch(F2,V2,'rw');
axisGeom; camlight headlight;
axis(axisLim(V1,V2));
gdrawnow;

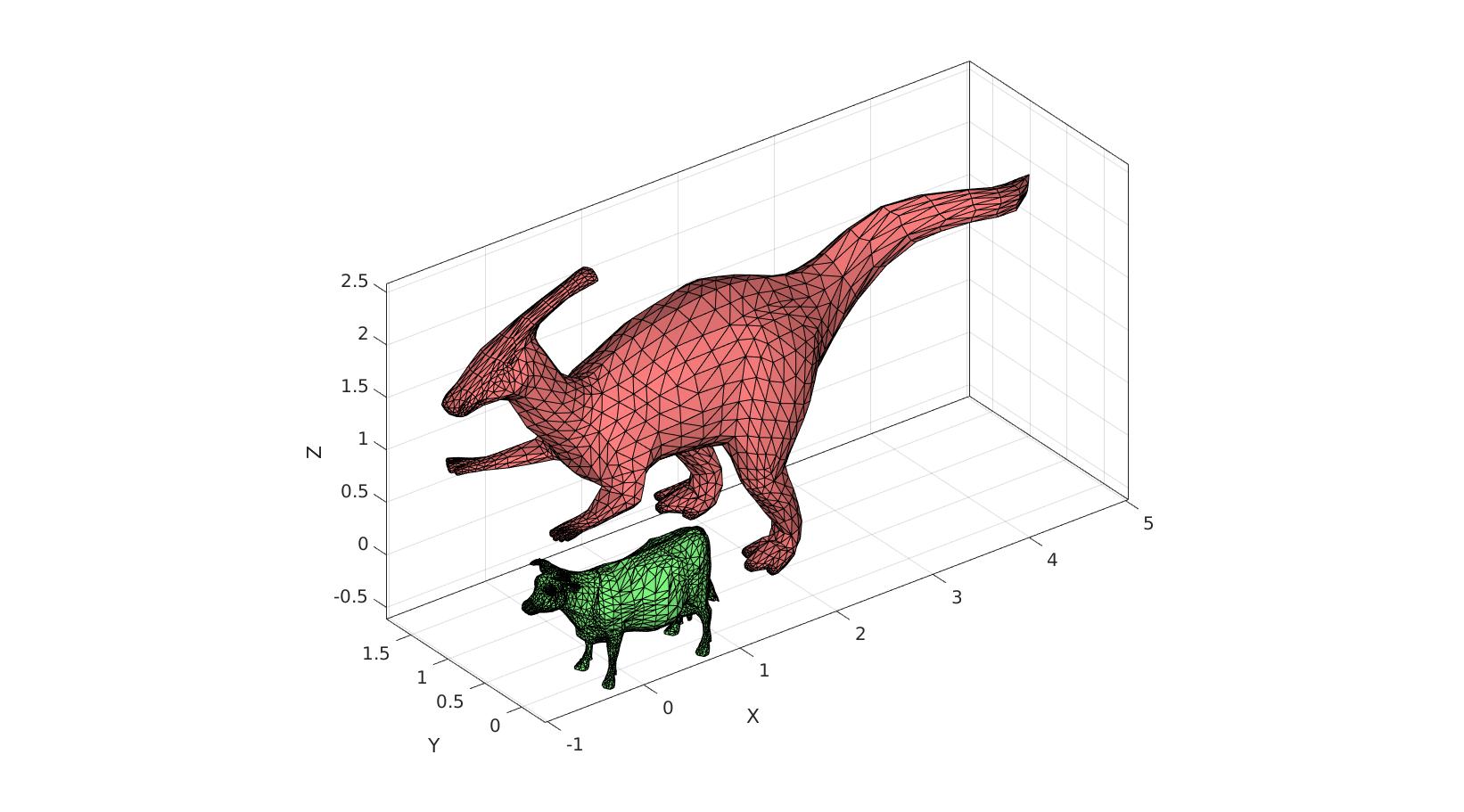
Example 3: setting axis limits tightly around multiple coordinate sets with varying dimensions

Create example data

V1=r.*[cos(t) sin(t)];
[F2,V2]=geoSphere(2,1);

Compute appropriate limits

axLim=axisLim(V1,V2) %Axis limits for vertices

axLim =

   -6.6976    6.7000   -5.8390    6.9989   -1.0000    1.0000

Assign axis limits using axisLim

cFigure; hold on;
plot(V1(:,1),V1(:,2),'b-');
gpatch(F2,V2,'rw');
axisGeom; camlight headlight;
axis(axisLim(V1,V2));
gdrawnow;

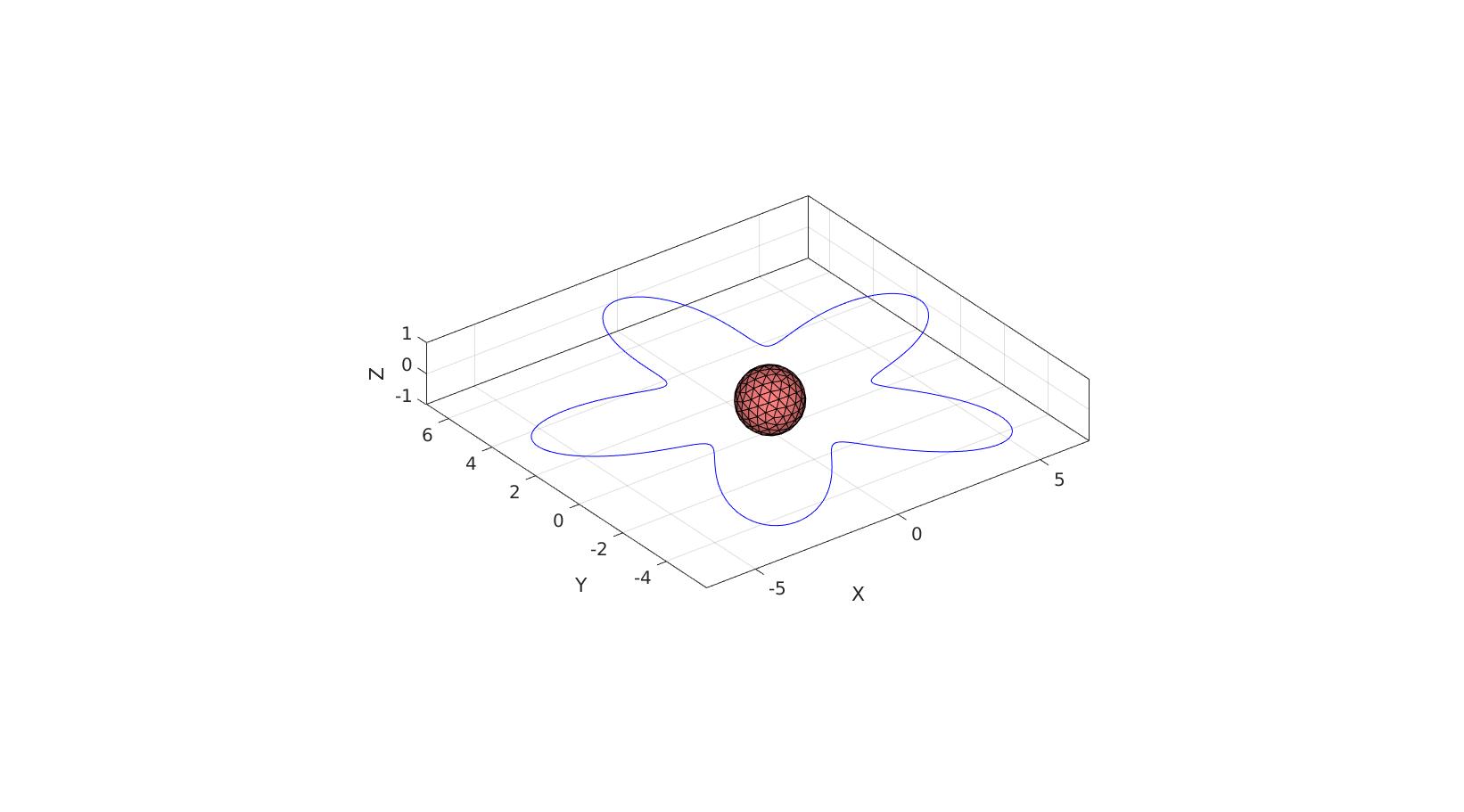
Example 4: setting axis limits tightly for coordinates over time

[F,V]=stanford_bunny; %Some graphics data

nSteps=50;
t=linspace(0,pi,nSteps)';
U=[-100*t/pi zeros(nSteps,1) 50*sin(t)];

V_DEF=zeros(size(V,1),3,nSteps);
for q=1:1:nSteps
    V_DEF(:,:,q)=V+U(q*ones(size(V,1),1),:);
end

Compute appropriate limits

axLim=axisLim(V_DEF) %Axis limits for vertices

axLim =

 -177.1042   77.6348  -59.4666   60.6226  -77.2629  125.9853

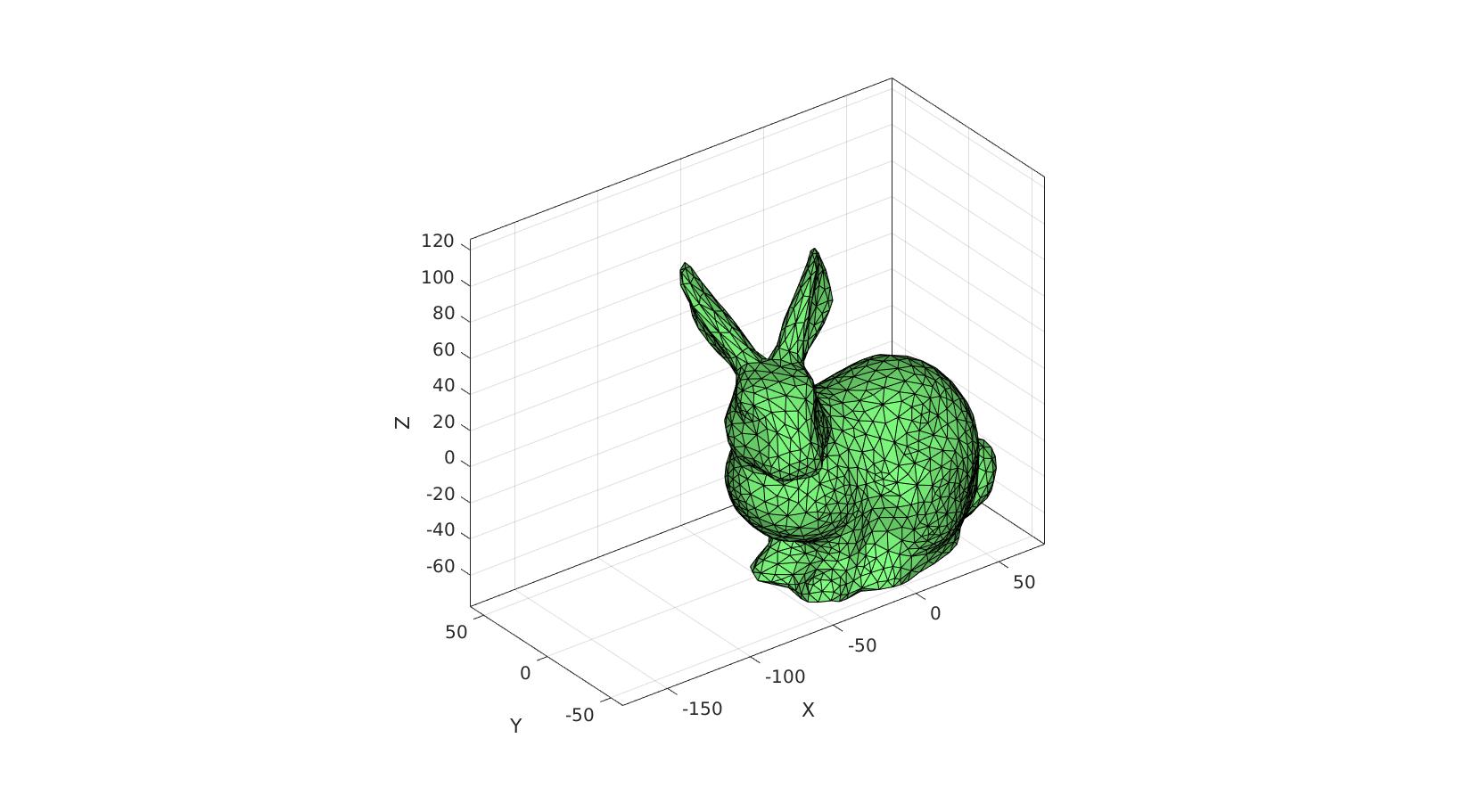
Assign axis limits using axisLim

hf=cFigure;
hp=gpatch(F,V,'gw');
axisGeom; camlight headlight;
axis(axisLim(V_DEF)); %Set limits to be suitable across time
drawnow;

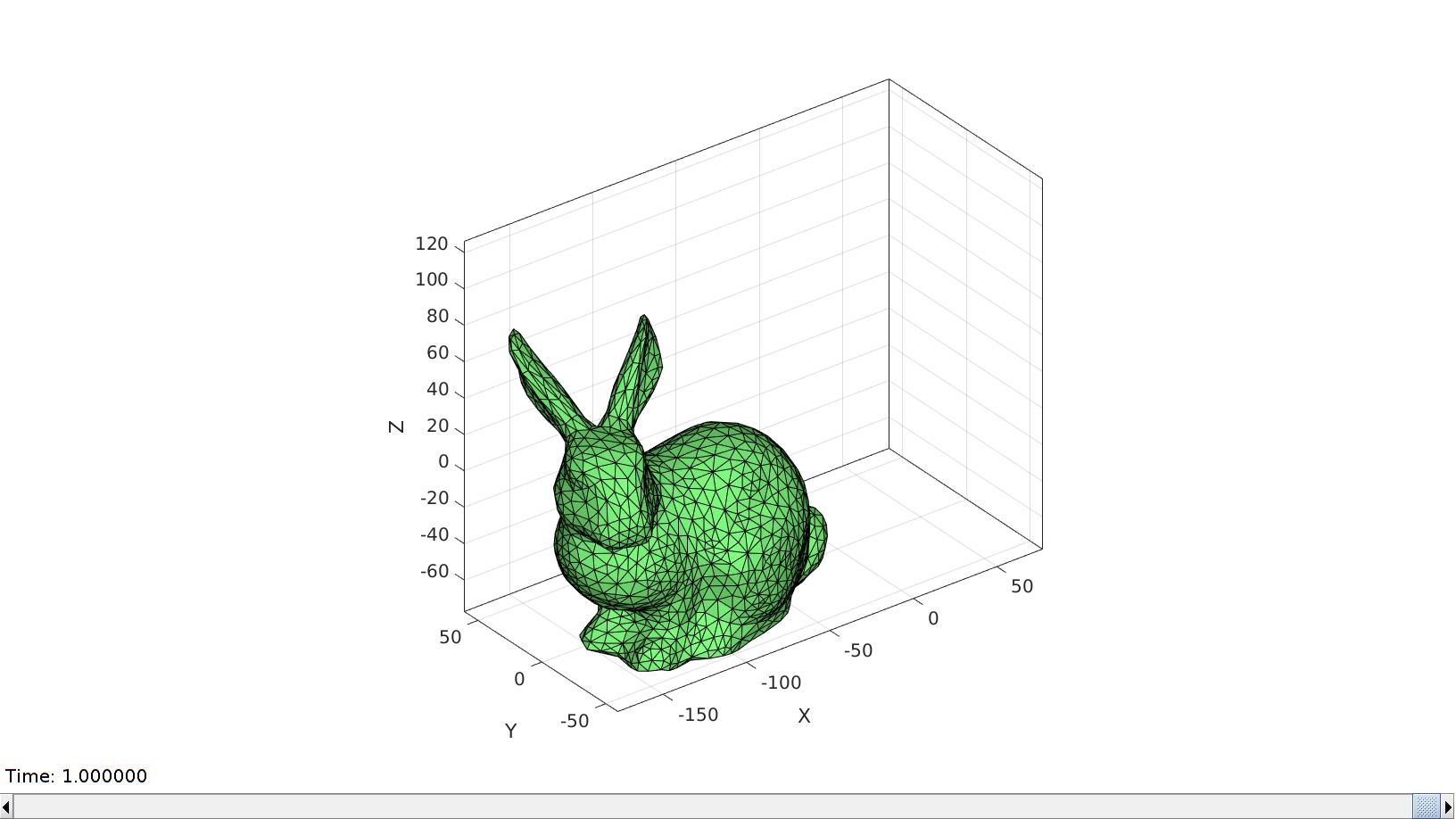
Use anim8 to animate the scene

animStruct.Time=linspace(0,1,nSteps); %Time vector

for q=1:1:nSteps
    %Set entries in animation structure
    animStruct.Handles{q}=hp; %Handles of objects to animate
    animStruct.Props{q}={'Vertices'}; %Properties of objects to animate
    animStruct.Set{q}={V_DEF(:,:,q)}; %Property values for to set in order to animate
end

% Start |anim8| gui
anim8(hf,animStruct);

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2006-2022 Kevin Mattheus Moerman and the GIBBON contributors

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2022b