subQuadCatmullClark

Below is a demonstration of the features of the subQuadCatmullClark function

Syntax
Description
Examples
Refining a cube using Catmull-Clark subdivision
Refining 3D quadrilateral surfaces with boundary edges
Refining 3D quadrilateral meshes using Catmull-Clark method
Example: Maintaining/resampling face data (e.g. face color)
Example: Maintaining/resampling vertex data (e.g. vertex color)
Refining a cube using Catmull-Clark subdivision
Example: Study vertex type

Syntax

[Fs,Vs]=subQuadCatmullClark(F,V,n);

Description

The subQuadCatmullClark function enables refinement of quadrangulated data. The quadrilateral faces defined by the patch format data F (faces) and V (vertices). Each face is split n times using the specified split method (splitMethod). The user may request the following outputs: The new faces: Fs The new coordinates: Vs Face color labels: C Nodal labels: CV

Four split methods are defined: 1: General linear resampling 2: Linear resampling only in the first direction 3: Linear resampling only in the second direction 4: Catmull-Clarke subdivision

Examples

clear; close all; clc;

Plot Settings

fontSize=15;
faceAlpha=1;
edgeColor=0.2*ones(1,3);
edgeWidth=1.5;
markerSize=35;
markerSize2=20;

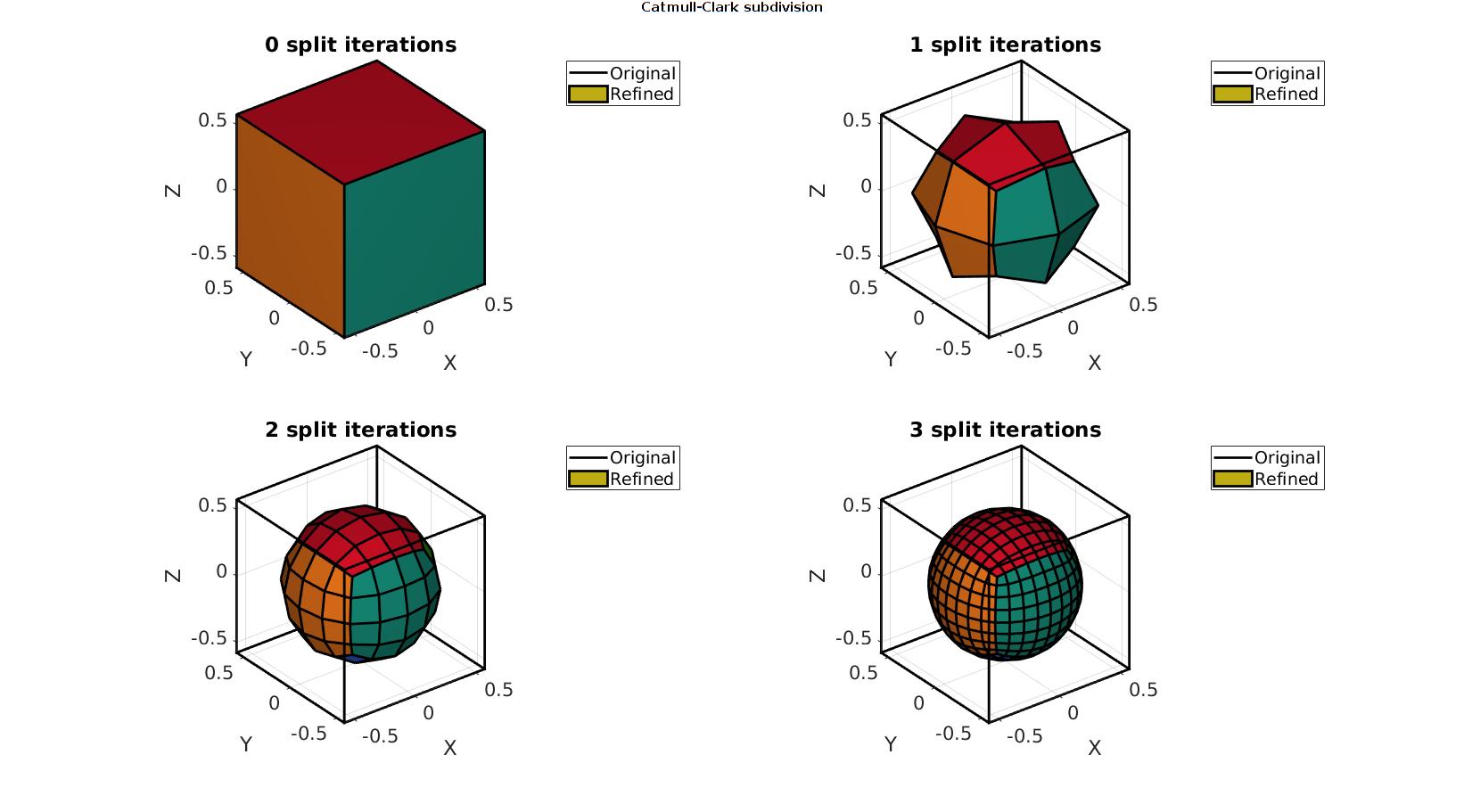
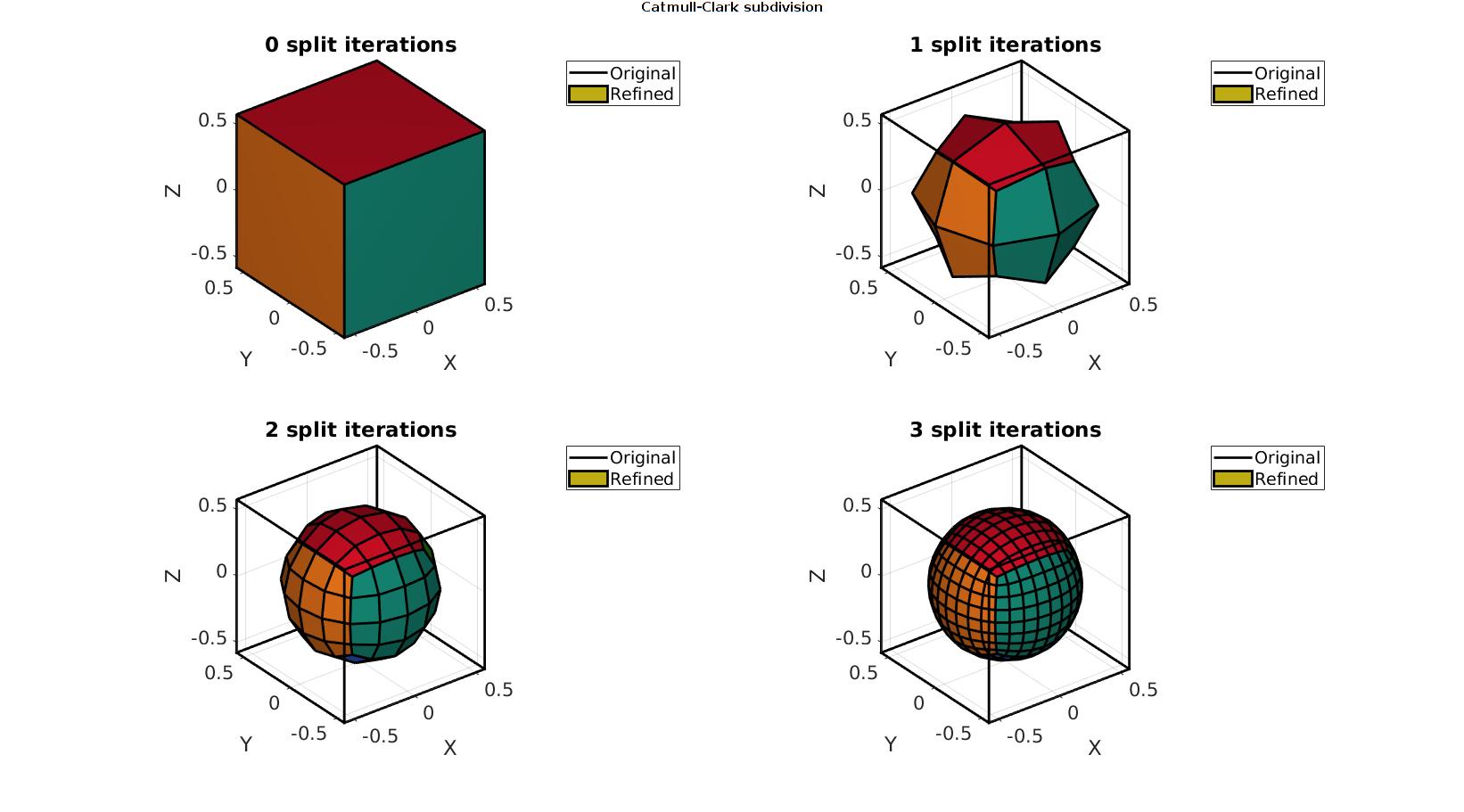
Refining a cube using Catmull-Clark subdivision

[V,F]=platonic_solid(2,1);

n=0:1:3; %Number of refinement steps

cFigure;
gtitle('Catmull-Clark subdivision')
for q=1:1:numel(n)
    [Fs,Vs,Cs]=subQuadCatmullClark(F,V,n(q));
    subplot(2,2,q); hold on;
    title([num2str(n(q)),' split iterations'],'FontSize',fontSize);
    hp1=gpatch(F,V,'none','k',1,2);
    hp2=gpatch(Fs,Vs,Cs,'k',1,2);
    colormap(gjet(6));
    axisGeom(gca,fontSize); camlight headlight;
    legend([hp1 hp2],{'Original','Refined'})
end
drawnow;

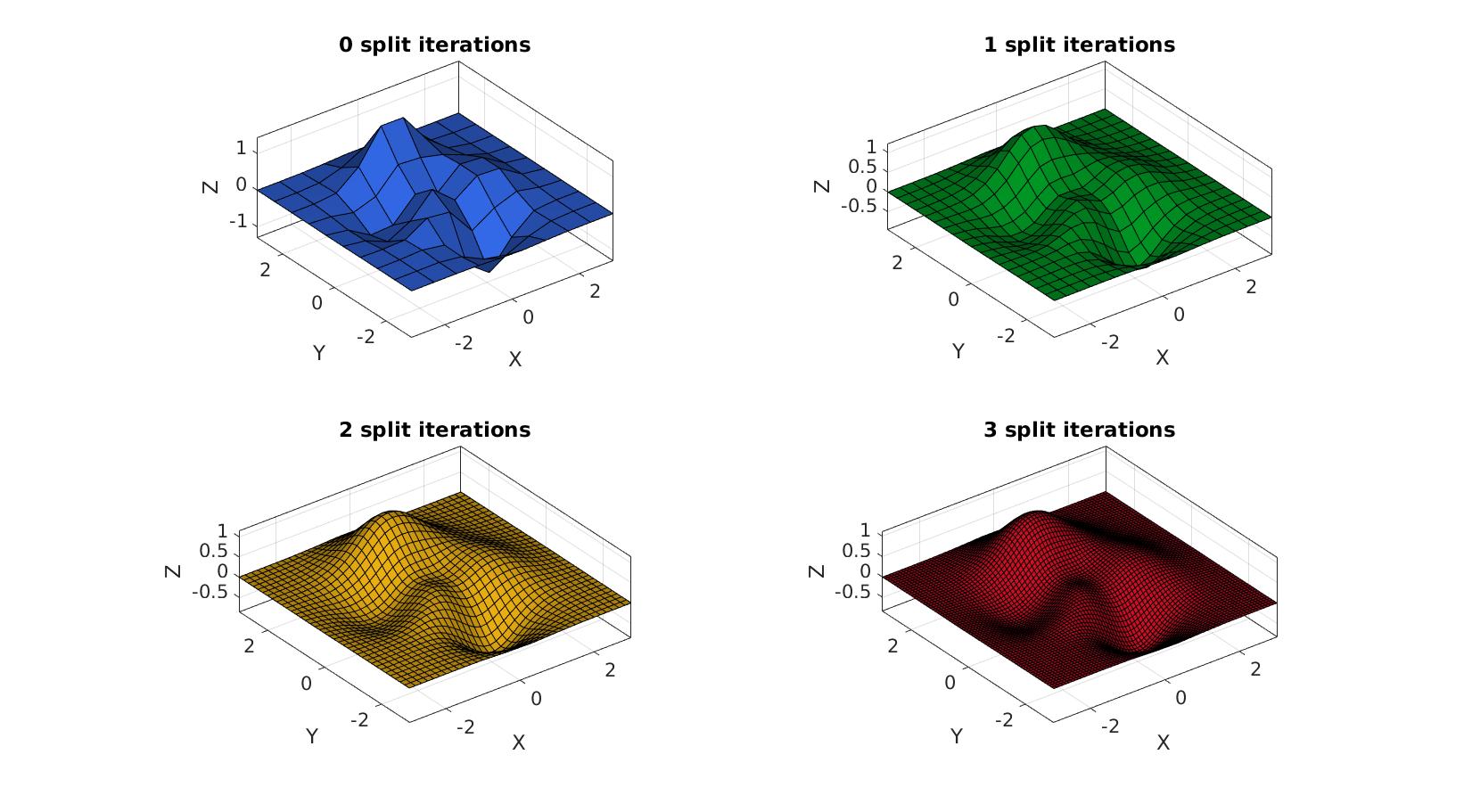
Refining 3D quadrilateral surfaces with boundary edges

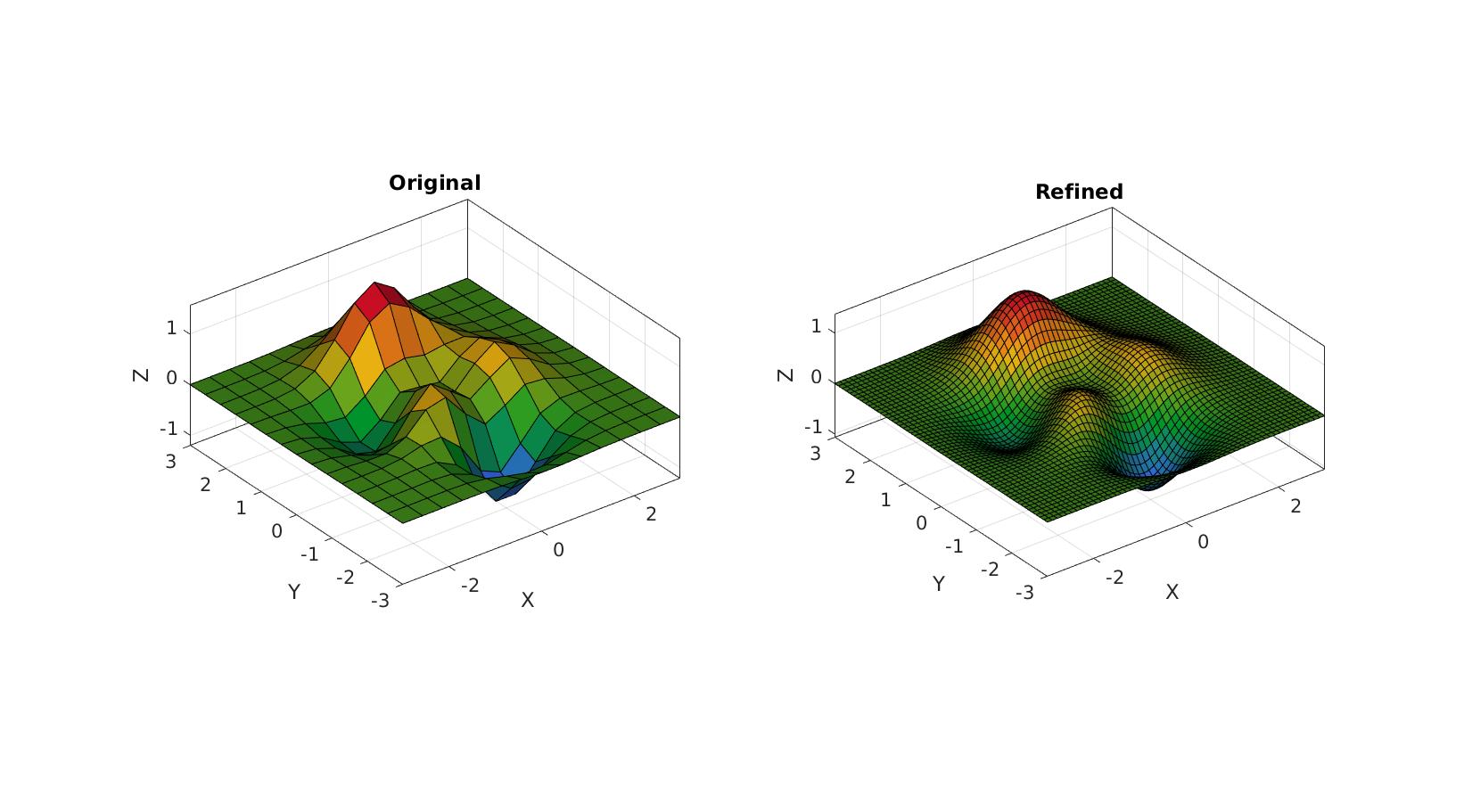
[X,Y,Z]=peaks(10);
Z=Z/5;
[F,V]=surf2patch(X,Y,Z);

n=[0 1 2 3]; %Number of refinement steps

fixBoundaryOpt=1;

pColors=gjet(numel(n));

cFigure;
for q=1:1:numel(n)
    [Fs,Vs]=subQuadCatmullClark(F,V,n(q),fixBoundaryOpt);
    subplot(2,2,q); hold on;
    title([num2str(n(q)),' split iterations'],'FontSize',fontSize);
    gpatch(Fs,Vs,pColors(q,:),'k');
%     patchNormPlot(Fs,Vs);
    axisGeom(gca,fontSize);
    camlight headlight;
end
drawnow;

Refining 3D quadrilateral meshes using Catmull-Clark method

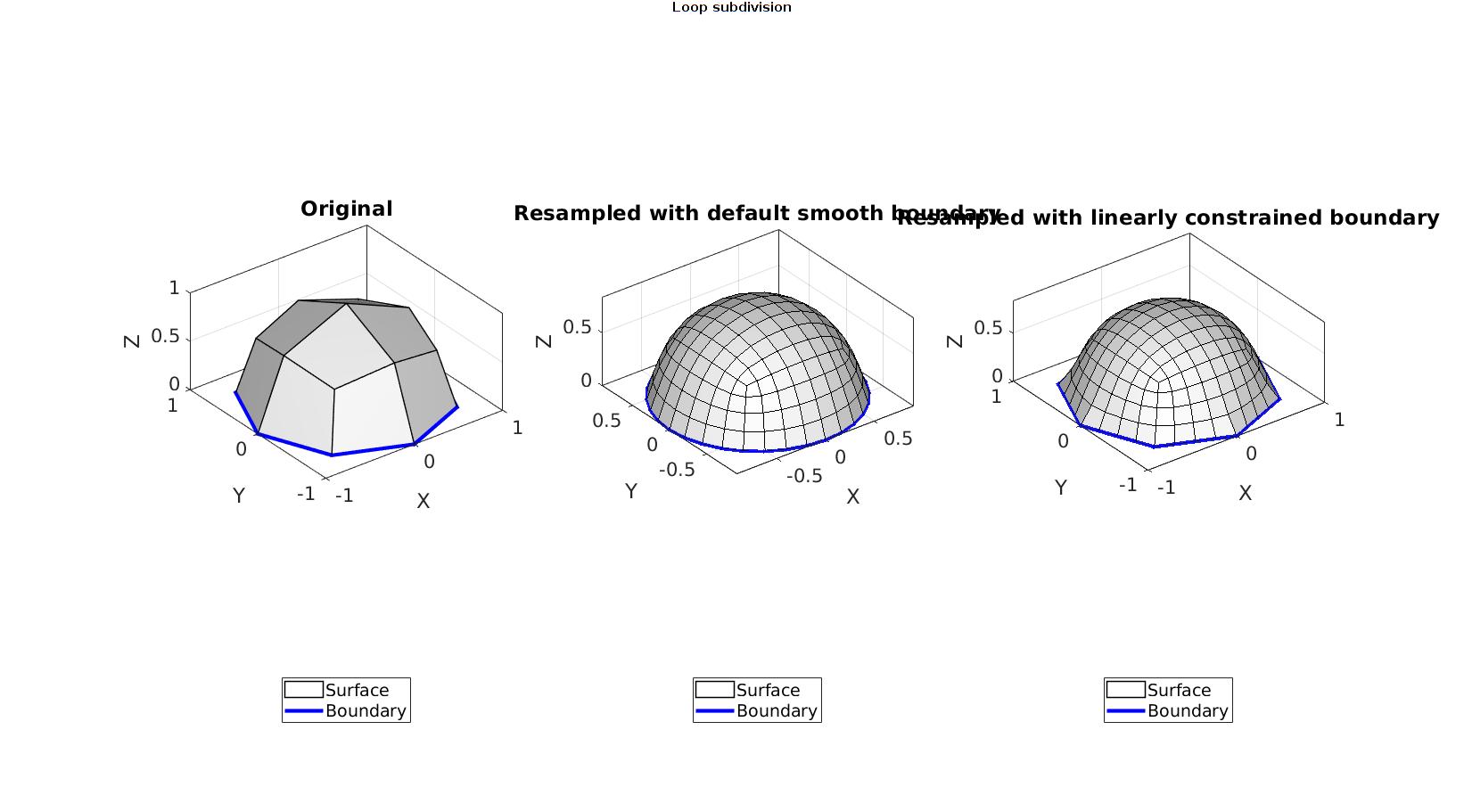
%Create example data with boundary edges (half-sphere)
[F,V]=quadSphere(1,1);
VF=patchCentre(F,V);
logicKeep=VF(:,3)>0;
F=F(logicKeep,:);
[F,V]=patchCleanUnused(F,V);

n=2; %Number of refinement steps
fixBoundaryOpt=0;
[Fs,Vs]=subQuadCatmullClark(F,V,n,fixBoundaryOpt);

fixBoundaryOpt=1; %Option to constrain boundary to be linearly sampled
[Fs2,Vs2]=subQuadCatmullClark(F,V,n,fixBoundaryOpt);

cFigure;
gtitle('Loop subdivision')
subplot(1,3,1); hold on;
title('Original','FontSize',fontSize);
hp1=gpatch(F,V,'w','k',1,1);
hp2=gpatch(patchBoundary(F,V),V,'none','b',1,3);
axisGeom(gca,fontSize); camlight headlight;
legend([hp1 hp2],{'Surface','Boundary'},'Location','SouthOutside');

subplot(1,3,2); hold on;
title('Resampled with default smooth boundary','FontSize',fontSize);
hp1=gpatch(Fs,Vs,'w','k',1,1);
hp2=gpatch(patchBoundary(Fs,Vs),Vs,'none','b',1,3); hp2.EdgeAlpha=0.9;
axisGeom(gca,fontSize); camlight headlight;
legend([hp1 hp2],{'Surface','Boundary'},'Location','SouthOutside');

subplot(1,3,3); hold on;
title('Resampled with linearly constrained boundary','FontSize',fontSize);
hp1=gpatch(Fs2,Vs2,'w','k',1,1);
hp2=gpatch(patchBoundary(Fs2,Vs2),Vs2,'none','b',1,3); hp2.EdgeAlpha=0.9;
axisGeom(gca,fontSize); camlight headlight;
legend([hp1 hp2],{'Surface','Boundary'},'Location','SouthOutside');

drawnow;

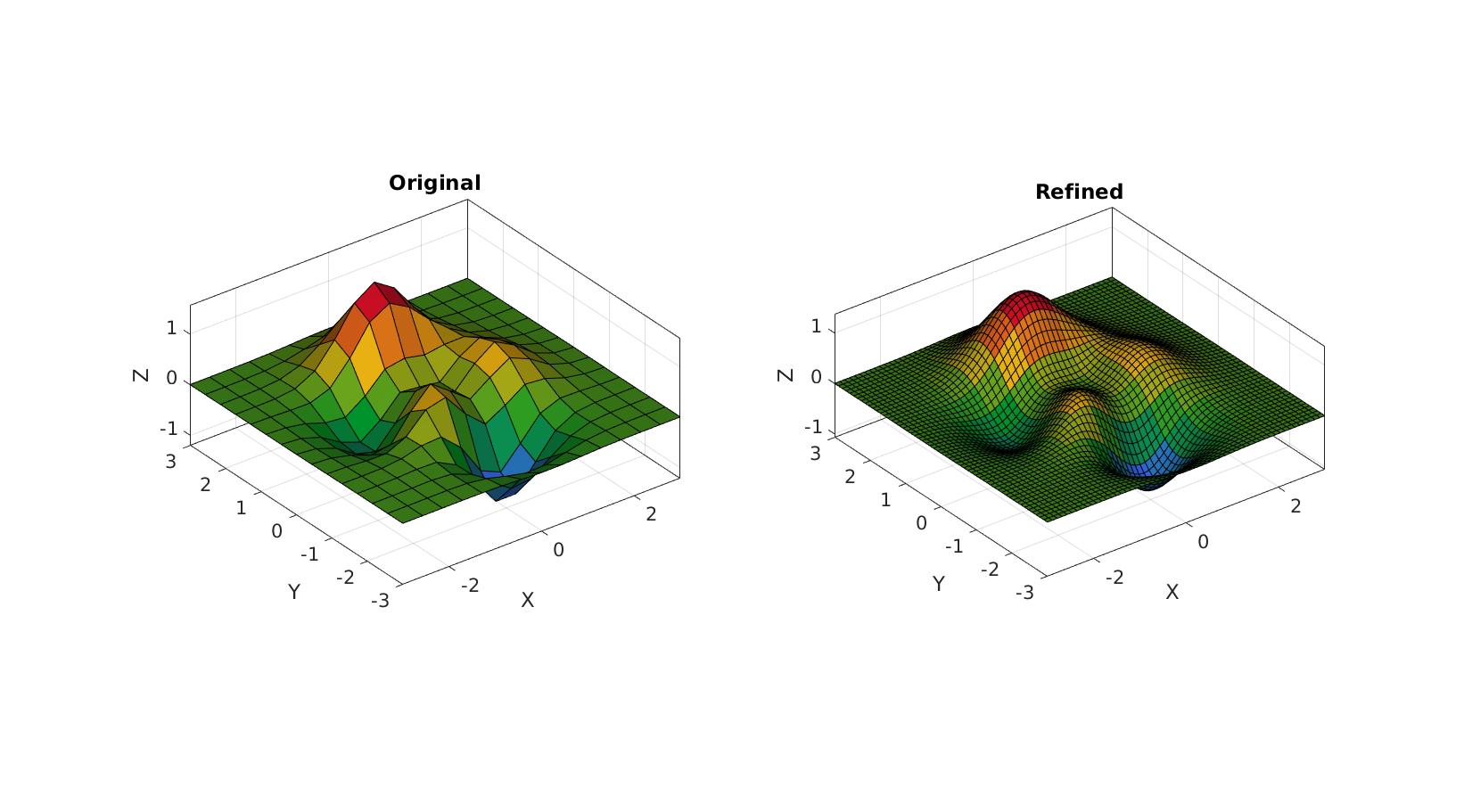
Example: Maintaining/resampling face data (e.g. face color)

[X,Y,Z]=peaks(15); Z=Z/5;
[F,V,CV]=surf2patch(X,Y,Z,Z);
C=vertexToFaceMeasure(F,CV);

Requesting additional output to allow for "book keeping" of face data

[Fs,Vs,Css]=subQuadCatmullClark(F,V,2,1);

The additional output Css contains face indices, i.e. each refined face in Fs belongs to an initial face in F and this mapping is defined in Css. Hence the following operation "picks" out the appropriate color data for each face from the original array.

Cs=C(Css); %Get colors for refined faces from color data of original

cFigure;
subplot(1,2,1); hold on;
title('Original','FontSize',fontSize);
gpatch(F,V,C,'k');
axisGeom(gca,fontSize);
colormap gjet;
camlight headlight;

subplot(1,2,2); hold on;
title('Refined','FontSize',fontSize);
gpatch(Fs,Vs,Cs,'k');
axisGeom(gca,fontSize);
colormap gjet;
camlight headlight;

drawnow;

Example: Maintaining/resampling vertex data (e.g. vertex color)

Requesting additional output to allow for "book keeping" of face data

VI=[V CV]; %Append color as artificial additional coordinate
[Fs,VsI]=subQuadCatmullClark(F,VI,2,1); %Refinement
Vs=VsI(:,1:3); %Pick out coordinates from first 3 columns
CVs=VsI(:,4); %Pick out resampled vertex data from 4th column

cFigure;
subplot(1,2,1); hold on;
title('Original','FontSize',fontSize);
gpatch(F,V,C,'k');
axisGeom(gca,fontSize);
colormap gjet;
camlight headlight;

subplot(1,2,2); hold on;
title('Refined','FontSize',fontSize);
gpatch(Fs,Vs,CVs,'k');
axisGeom(gca,fontSize);
colormap gjet;
camlight headlight;

drawnow;

Refining a cube using Catmull-Clark subdivision

[V,F]=platonic_solid(2,1);

n=0:1:3; %Number of refinement steps

cFigure;
gtitle('Catmull-Clark subdivision')
for q=1:1:numel(n)
    [Fs,Vs,Cs]=subQuadCatmullClark(F,V,n(q));
    subplot(2,2,q); hold on;
    title([num2str(n(q)),' split iterations'],'FontSize',fontSize);
    hp1=gpatch(F,V,'none','k',1,2);
    hp2=gpatch(Fs,Vs,Cs,'k',1,2);
    colormap(gjet(6));
    axisGeom(gca,fontSize); camlight headlight;
    legend([hp1 hp2],{'Original','Refined'})
end
drawnow;

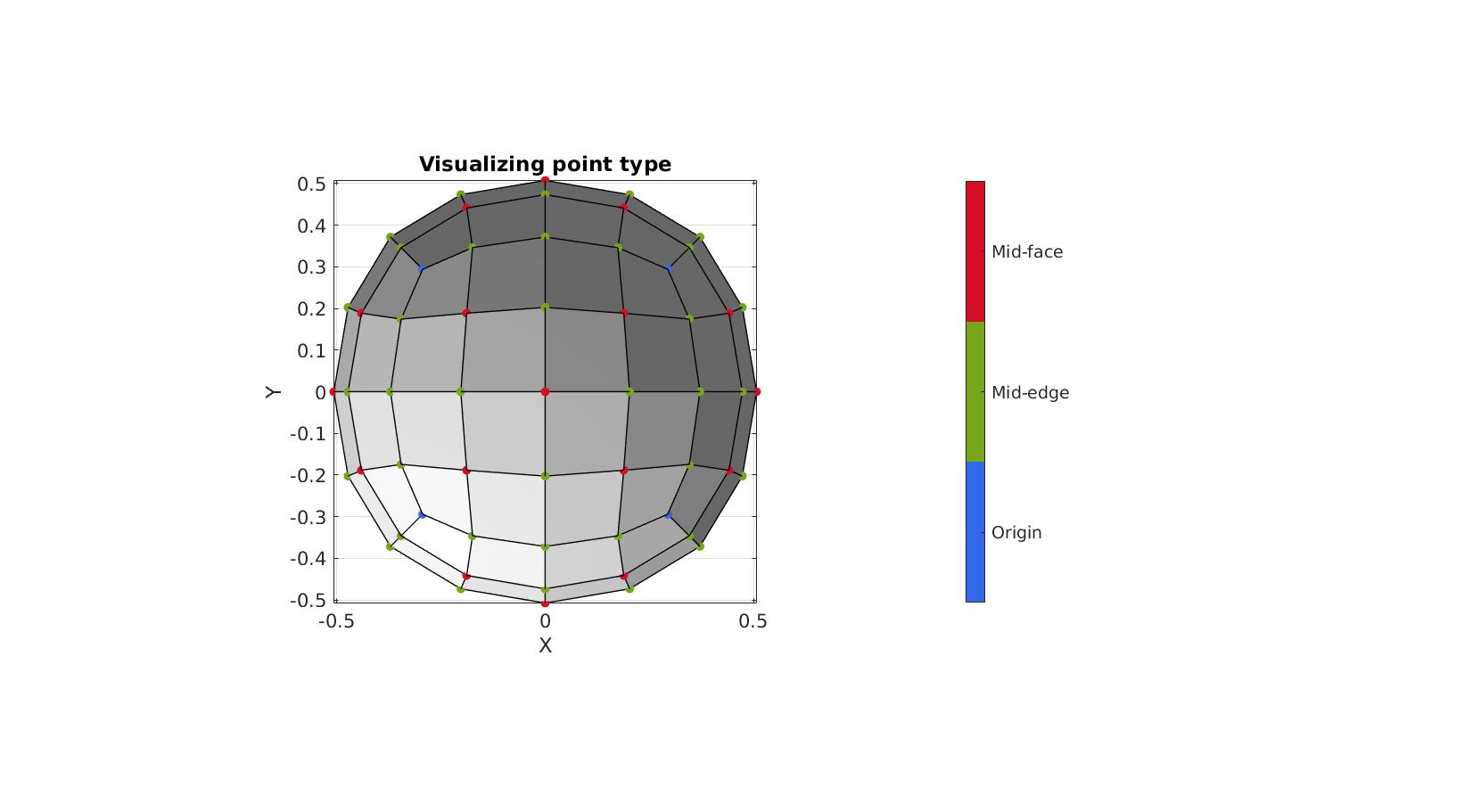
Example: Study vertex type

An optional 4th output can provide "vertex labels", these define the vertex origins, i.e. whether they stem from the initial coordinates (iteration 0), or from iteration n.

n=2; %Number of refinement steps
[Fs,Vs,~,CV]=subQuadCatmullClark(F,V,n);

cFigure; hold on;
title('Visualizing point type','FontSize',fontSize);
gpatch(Fs,Vs,'w','k',1,1);
scatterV(Vs,50,CV,'filled')
axisGeom(gca,fontSize); camlight headlight;
view(2);
colormap gjet; [~,hc]=icolorbar;
hc.TickLabels={'Origin';'Mid-edge';'Mid-face'};
drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

subQuadCatmullClark

Contents

Syntax

Description

Examples

Refining a cube using Catmull-Clark subdivision

Refining 3D quadrilateral surfaces with boundary edges

Refining 3D quadrilateral meshes using Catmull-Clark method

Example: Maintaining/resampling face data (e.g. face color)

Example: Maintaining/resampling vertex data (e.g. vertex color)

Refining a cube using Catmull-Clark subdivision

Example: Study vertex type