pointSetPrincipalDir
Below is a demonstration of the features of the pointSetPrincipalDir function
Contents
clear; close all; clc;
Syntax
[V,S,U]=pointSetPrincipalDir(X)
Description
Examples
Plot settings
fontSize=15; markerSize=25;
Using pointSetPrincipalDir to determine main directions of a point cloud
Simulating an ellipsoid with known directions
% Ellipsoid axis stretch factors ellipStretchTrue=[pi 2 1] % Create ellipsoid patch data [F,V,~]=geoSphere(3,1); V=V.*ellipStretchTrue(ones(size(V,1),1),:); %Create Euler angles to set directions E=[-0.25*pi 0.25*pi 0.25*pi]; [R_true,~]=euler2DCM(E); %The true directions for X, Y and Z axis V=(R_true*V')'; %Rotate polyhedron
ellipStretchTrue =
3.1416 2.0000 1.0000
This is the true axis system
R_true
R_true =
0.5000 -0.5000 0.7071
0.1464 0.8536 0.5000
-0.8536 -0.1464 0.5000
Determine principal directions of the point set (in this case an ellipsoidal polyhedron).
[R_fit]=pointSetPrincipalDir(V)
R_fit =
0.5000 -0.5000 0.7071
0.1464 0.8536 0.5000
-0.8536 -0.1464 0.5000
Visualizing results
cFigure; hold on; gtitle('The polyhedron with true (transparant) and determined (solid) axis directions',fontSize); gpatch(F,V,0.75*ones(1,3),'none',0.5); plotV(V,'k.','MarkerSize',markerSize); hl1=quiverTriad(mean(V,1),R_true,10,[],0.2); hl2=quiverTriad(mean(V,1),R_fit,7,[],1); legend([hl1 hl2],{'True directions','Fitted directions'}); camlight('headlight'); axisGeom(gca,fontSize); drawnow;
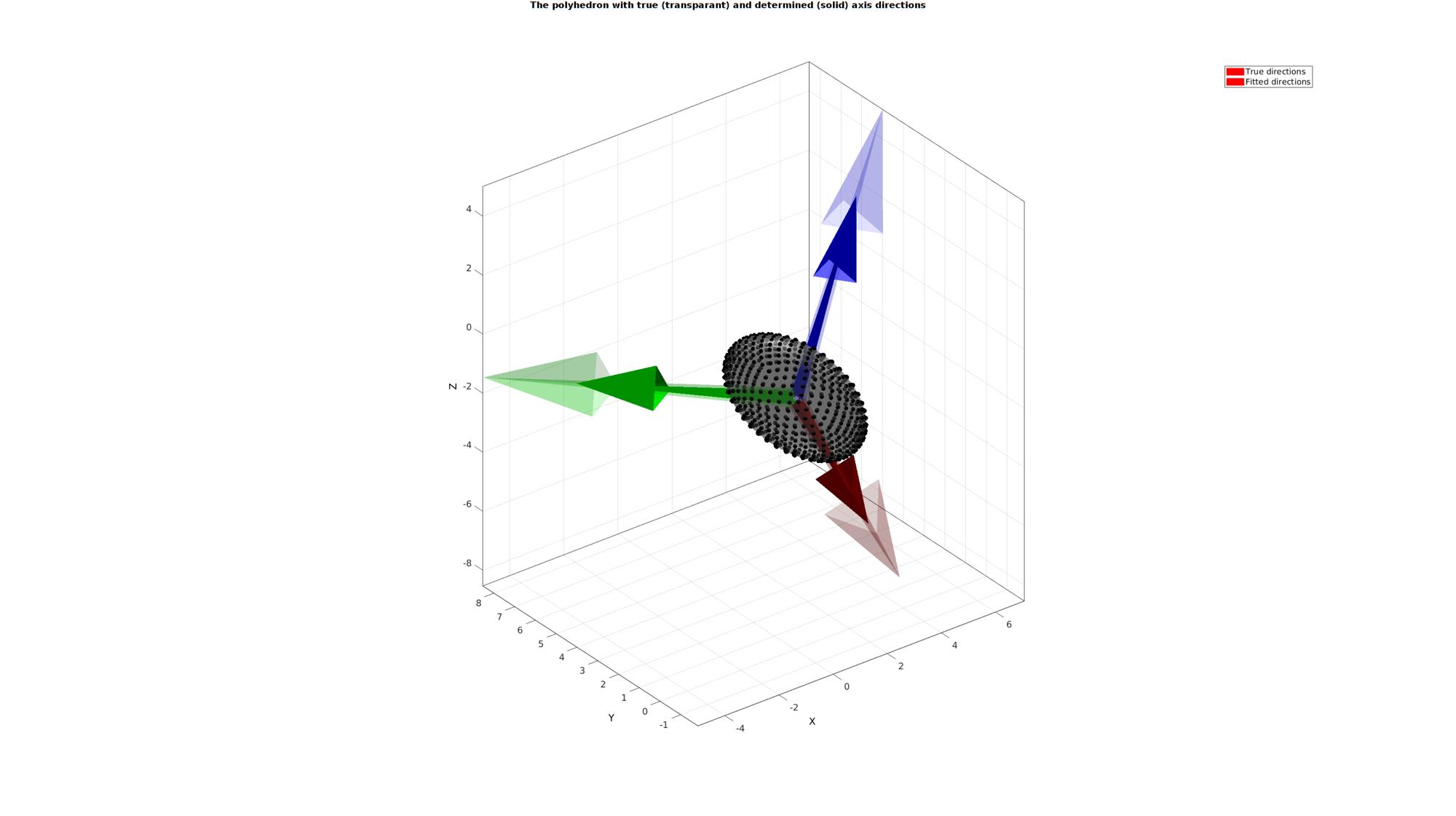
Output of the singular value decomposition data data
[R_fit,S,U]=pointSetPrincipalDir(V)
R_fit =
0.5000 -0.5000 0.7071
0.1464 0.8536 0.5000
-0.8536 -0.1464 0.5000
S =
45.9575 0 0
0 29.2575 0
0 0 14.6287
U =
0.0000 -0.0359 -0.0581
-0.0000 -0.0359 0.0581
0.0000 0.0359 0.0581
-0.0000 0.0359 -0.0581
-0.0359 -0.0581 -0.0000
-0.0359 0.0581 0.0000
0.0359 0.0581 0.0000
0.0359 -0.0581 -0.0000
-0.0581 0.0000 -0.0359
0.0581 0.0000 -0.0359
0.0581 -0.0000 0.0359
-0.0581 -0.0000 0.0359
0.0000 0.0000 -0.0684
-0.0211 -0.0553 -0.0342
0.0211 -0.0553 -0.0342
-0.0342 -0.0211 -0.0553
0.0342 -0.0211 -0.0553
0.0000 -0.0000 0.0684
-0.0211 -0.0553 0.0342
0.0211 -0.0553 0.0342
0.0342 -0.0211 0.0553
-0.0342 -0.0211 0.0553
-0.0211 0.0553 0.0342
0.0211 0.0553 0.0342
0.0342 0.0211 0.0553
-0.0342 0.0211 0.0553
-0.0211 0.0553 -0.0342
0.0211 0.0553 -0.0342
-0.0342 0.0211 -0.0553
0.0342 0.0211 -0.0553
-0.0000 -0.0684 -0.0000
-0.0553 -0.0342 -0.0211
-0.0553 -0.0342 0.0211
-0.0000 0.0684 0.0000
-0.0553 0.0342 -0.0211
-0.0553 0.0342 0.0211
0.0553 0.0342 -0.0211
0.0553 0.0342 0.0211
0.0553 -0.0342 -0.0211
0.0553 -0.0342 0.0211
-0.0684 0.0000 -0.0000
0.0684 -0.0000 0.0000
0.0000 -0.0187 -0.0658
-0.0110 -0.0474 -0.0480
0.0110 -0.0474 -0.0480
-0.0178 -0.0297 -0.0590
0.0178 -0.0297 -0.0590
0.0000 -0.0187 0.0658
-0.0110 -0.0474 0.0480
0.0110 -0.0474 0.0480
0.0178 -0.0297 0.0590
-0.0178 -0.0297 0.0590
0.0000 0.0187 0.0658
-0.0110 0.0474 0.0480
0.0110 0.0474 0.0480
0.0178 0.0297 0.0590
-0.0178 0.0297 0.0590
-0.0000 0.0187 -0.0658
-0.0110 0.0474 -0.0480
0.0110 0.0474 -0.0480
-0.0178 0.0297 -0.0590
0.0178 0.0297 -0.0590
-0.0297 -0.0590 -0.0178
-0.0297 -0.0590 0.0178
-0.0187 -0.0658 -0.0000
-0.0474 -0.0480 -0.0110
-0.0474 -0.0480 0.0110
-0.0297 0.0590 0.0178
-0.0297 0.0590 -0.0178
-0.0187 0.0658 0.0000
-0.0474 0.0480 -0.0110
-0.0474 0.0480 0.0110
0.0297 0.0590 0.0178
0.0297 0.0590 -0.0178
0.0187 0.0658 0.0000
0.0474 0.0480 -0.0110
0.0474 0.0480 0.0110
0.0297 -0.0590 -0.0178
0.0297 -0.0590 0.0178
0.0187 -0.0658 -0.0000
0.0474 -0.0480 -0.0110
0.0474 -0.0480 0.0110
-0.0480 -0.0110 -0.0474
-0.0480 0.0110 -0.0474
-0.0590 -0.0178 -0.0297
-0.0590 0.0178 -0.0297
-0.0658 0.0000 -0.0187
0.0480 -0.0110 -0.0474
0.0480 0.0110 -0.0474
0.0590 0.0178 -0.0297
0.0590 -0.0178 -0.0297
0.0658 -0.0000 -0.0187
0.0480 -0.0110 0.0474
0.0480 0.0110 0.0474
0.0590 0.0178 0.0297
0.0590 -0.0178 0.0297
0.0658 -0.0000 0.0187
-0.0480 -0.0110 0.0474
-0.0480 0.0110 0.0474
-0.0590 -0.0178 0.0297
-0.0590 0.0178 0.0297
-0.0658 0.0000 0.0187
-0.0180 -0.0111 -0.0650
0.0180 -0.0111 -0.0650
-0.0180 0.0111 -0.0650
0.0180 0.0111 -0.0650
-0.0000 -0.0581 -0.0359
-0.0291 -0.0402 -0.0470
-0.0111 -0.0650 -0.0180
-0.0402 -0.0470 -0.0291
0.0291 -0.0402 -0.0470
0.0111 -0.0650 -0.0180
0.0402 -0.0470 -0.0291
-0.0359 0.0000 -0.0581
-0.0470 -0.0291 -0.0402
0.0359 0.0000 -0.0581
0.0470 -0.0291 -0.0402
0.0180 -0.0111 0.0650
-0.0180 -0.0111 0.0650
0.0180 0.0111 0.0650
-0.0180 0.0111 0.0650
0.0000 -0.0581 0.0359
-0.0291 -0.0402 0.0470
-0.0111 -0.0650 0.0180
-0.0402 -0.0470 0.0291
0.0291 -0.0402 0.0470
0.0111 -0.0650 0.0180
0.0402 -0.0470 0.0291
0.0359 -0.0000 0.0581
0.0470 -0.0291 0.0402
-0.0359 -0.0000 0.0581
-0.0470 -0.0291 0.0402
0.0000 0.0581 0.0359
-0.0291 0.0402 0.0470
-0.0111 0.0650 0.0180
-0.0402 0.0470 0.0291
0.0291 0.0402 0.0470
0.0111 0.0650 0.0180
0.0402 0.0470 0.0291
0.0470 0.0291 0.0402
-0.0470 0.0291 0.0402
-0.0000 0.0581 -0.0359
-0.0291 0.0402 -0.0470
-0.0111 0.0650 -0.0180
-0.0402 0.0470 -0.0291
0.0291 0.0402 -0.0470
0.0111 0.0650 -0.0180
0.0402 0.0470 -0.0291
-0.0470 0.0291 -0.0402
0.0470 0.0291 -0.0402
-0.0581 -0.0359 0.0000
-0.0650 -0.0180 -0.0111
-0.0650 -0.0180 0.0111
-0.0581 0.0359 -0.0000
-0.0650 0.0180 -0.0111
-0.0650 0.0180 0.0111
0.0581 0.0359 0.0000
0.0650 0.0180 -0.0111
0.0650 0.0180 0.0111
0.0581 -0.0359 0.0000
0.0650 -0.0180 -0.0111
0.0650 -0.0180 0.0111
-0.0000 -0.0276 -0.0626
-0.0055 -0.0421 -0.0536
0.0055 -0.0421 -0.0536
-0.0090 -0.0331 -0.0591
0.0090 -0.0331 -0.0591
0.0000 -0.0276 0.0626
-0.0055 -0.0421 0.0536
0.0055 -0.0421 0.0536
0.0090 -0.0331 0.0591
-0.0090 -0.0331 0.0591
0.0000 0.0276 0.0626
-0.0055 0.0421 0.0536
0.0055 0.0421 0.0536
0.0090 0.0331 0.0591
-0.0090 0.0331 0.0591
0.0000 0.0276 -0.0626
-0.0055 0.0421 -0.0536
0.0055 0.0421 -0.0536
-0.0090 0.0331 -0.0591
0.0090 0.0331 -0.0591
-0.0331 -0.0591 -0.0090
-0.0331 -0.0591 0.0090
-0.0276 -0.0626 -0.0000
-0.0421 -0.0536 -0.0055
-0.0421 -0.0536 0.0055
-0.0331 0.0591 0.0090
-0.0331 0.0591 -0.0090
-0.0276 0.0626 0.0000
-0.0421 0.0536 -0.0055
-0.0421 0.0536 0.0055
0.0331 0.0591 0.0090
0.0331 0.0591 -0.0090
0.0276 0.0626 0.0000
0.0421 0.0536 -0.0055
0.0421 0.0536 0.0055
0.0331 -0.0591 -0.0090
0.0331 -0.0591 0.0090
0.0276 -0.0626 -0.0000
0.0421 -0.0536 -0.0055
0.0421 -0.0536 0.0055
-0.0536 -0.0055 -0.0421
-0.0536 0.0055 -0.0421
-0.0591 -0.0090 -0.0331
-0.0591 0.0090 -0.0331
-0.0626 0.0000 -0.0276
0.0536 -0.0055 -0.0421
0.0536 0.0055 -0.0421
0.0591 0.0090 -0.0331
0.0591 -0.0090 -0.0331
0.0626 0.0000 -0.0276
0.0536 -0.0055 0.0421
0.0536 0.0055 0.0421
0.0591 0.0090 0.0331
0.0591 -0.0090 0.0331
0.0626 -0.0000 0.0276
-0.0536 -0.0055 0.0421
-0.0536 0.0055 0.0421
-0.0591 -0.0090 0.0331
-0.0591 0.0090 0.0331
-0.0626 -0.0000 0.0276
-0.0000 -0.0094 -0.0677
0.0000 0.0094 -0.0677
-0.0091 -0.0056 -0.0675
0.0091 -0.0056 -0.0675
-0.0091 0.0056 -0.0675
0.0091 0.0056 -0.0675
-0.0162 -0.0519 -0.0415
-0.0256 -0.0577 -0.0262
-0.0107 -0.0574 -0.0355
-0.0254 -0.0483 -0.0411
-0.0163 -0.0609 -0.0264
-0.0310 -0.0518 -0.0320
0.0162 -0.0519 -0.0415
0.0256 -0.0577 -0.0262
0.0107 -0.0574 -0.0355
0.0254 -0.0483 -0.0411
0.0163 -0.0609 -0.0264
0.0310 -0.0518 -0.0320
-0.0262 -0.0256 -0.0577
-0.0415 -0.0162 -0.0519
-0.0264 -0.0163 -0.0609
-0.0320 -0.0310 -0.0518
-0.0355 -0.0107 -0.0574
-0.0411 -0.0254 -0.0483
0.0262 -0.0256 -0.0577
0.0415 -0.0162 -0.0519
0.0264 -0.0163 -0.0609
0.0320 -0.0310 -0.0518
0.0355 -0.0107 -0.0574
0.0411 -0.0254 -0.0483
0.0000 -0.0094 0.0677
0.0000 0.0094 0.0677
0.0091 -0.0056 0.0675
-0.0091 -0.0056 0.0675
0.0091 0.0056 0.0675
-0.0091 0.0056 0.0675
-0.0162 -0.0519 0.0415
-0.0256 -0.0577 0.0262
-0.0107 -0.0574 0.0355
-0.0254 -0.0483 0.0411
-0.0163 -0.0609 0.0264
-0.0310 -0.0518 0.0320
0.0162 -0.0519 0.0415
0.0256 -0.0577 0.0262
0.0107 -0.0574 0.0355
0.0254 -0.0483 0.0411
0.0163 -0.0609 0.0264
0.0310 -0.0518 0.0320
0.0262 -0.0256 0.0577
0.0415 -0.0162 0.0519
0.0264 -0.0163 0.0609
0.0320 -0.0310 0.0518
0.0355 -0.0107 0.0574
0.0411 -0.0254 0.0483
-0.0262 -0.0256 0.0577
-0.0415 -0.0162 0.0519
-0.0264 -0.0163 0.0609
-0.0320 -0.0310 0.0518
-0.0355 -0.0107 0.0574
-0.0411 -0.0254 0.0483
-0.0162 0.0519 0.0415
-0.0256 0.0577 0.0262
-0.0107 0.0574 0.0355
-0.0254 0.0483 0.0411
-0.0163 0.0609 0.0264
-0.0310 0.0518 0.0320
0.0162 0.0519 0.0415
0.0256 0.0577 0.0262
0.0107 0.0574 0.0355
0.0254 0.0483 0.0411
0.0163 0.0609 0.0264
0.0310 0.0518 0.0320
0.0262 0.0256 0.0577
0.0415 0.0162 0.0519
0.0264 0.0163 0.0609
0.0355 0.0107 0.0574
0.0320 0.0310 0.0518
0.0411 0.0254 0.0483
-0.0262 0.0256 0.0577
-0.0415 0.0162 0.0519
-0.0264 0.0163 0.0609
-0.0355 0.0107 0.0574
-0.0320 0.0310 0.0518
-0.0411 0.0254 0.0483
-0.0162 0.0519 -0.0415
-0.0256 0.0577 -0.0262
-0.0107 0.0574 -0.0355
-0.0254 0.0483 -0.0411
-0.0163 0.0609 -0.0264
-0.0310 0.0518 -0.0320
0.0162 0.0519 -0.0415
0.0256 0.0577 -0.0262
0.0107 0.0574 -0.0355
0.0254 0.0483 -0.0411
0.0163 0.0609 -0.0264
0.0310 0.0518 -0.0320
-0.0262 0.0256 -0.0577
-0.0415 0.0162 -0.0519
-0.0264 0.0163 -0.0609
-0.0355 0.0107 -0.0574
-0.0320 0.0310 -0.0518
-0.0411 0.0254 -0.0483
0.0262 0.0256 -0.0577
0.0415 0.0162 -0.0519
0.0264 0.0163 -0.0609
0.0355 0.0107 -0.0574
0.0320 0.0310 -0.0518
0.0411 0.0254 -0.0483
-0.0094 -0.0677 -0.0000
0.0094 -0.0677 0.0000
-0.0056 -0.0675 -0.0091
0.0056 -0.0675 -0.0091
-0.0056 -0.0675 0.0091
0.0056 -0.0675 0.0091
-0.0519 -0.0415 -0.0162
-0.0577 -0.0262 -0.0256
-0.0483 -0.0411 -0.0254
-0.0518 -0.0320 -0.0310
-0.0574 -0.0355 -0.0107
-0.0609 -0.0264 -0.0163
-0.0519 -0.0415 0.0162
-0.0577 -0.0262 0.0256
-0.0483 -0.0411 0.0254
-0.0518 -0.0320 0.0310
-0.0574 -0.0355 0.0107
-0.0609 -0.0264 0.0163
-0.0094 0.0677 0.0000
0.0094 0.0677 0.0000
-0.0056 0.0675 0.0091
0.0056 0.0675 0.0091
-0.0056 0.0675 -0.0091
0.0056 0.0675 -0.0091
-0.0519 0.0415 -0.0162
-0.0577 0.0262 -0.0256
-0.0483 0.0411 -0.0254
-0.0518 0.0320 -0.0310
-0.0574 0.0355 -0.0107
-0.0609 0.0264 -0.0163
-0.0519 0.0415 0.0162
-0.0577 0.0262 0.0256
-0.0483 0.0411 0.0254
-0.0518 0.0320 0.0310
-0.0574 0.0355 0.0107
-0.0609 0.0264 0.0163
0.0519 0.0415 -0.0162
0.0577 0.0262 -0.0256
0.0483 0.0411 -0.0254
0.0518 0.0320 -0.0310
0.0574 0.0355 -0.0107
0.0609 0.0264 -0.0163
0.0519 0.0415 0.0162
0.0577 0.0262 0.0256
0.0483 0.0411 0.0254
0.0518 0.0320 0.0310
0.0574 0.0355 0.0107
0.0609 0.0264 0.0163
0.0519 -0.0415 -0.0162
0.0577 -0.0262 -0.0256
0.0483 -0.0411 -0.0254
0.0518 -0.0320 -0.0310
0.0574 -0.0355 -0.0107
0.0609 -0.0264 -0.0163
0.0519 -0.0415 0.0162
0.0577 -0.0262 0.0256
0.0483 -0.0411 0.0254
0.0518 -0.0320 0.0310
0.0574 -0.0355 0.0107
0.0609 -0.0264 0.0163
-0.0677 0.0000 -0.0094
-0.0677 0.0000 0.0094
-0.0675 -0.0091 -0.0056
-0.0675 -0.0091 0.0056
-0.0675 0.0091 -0.0056
-0.0675 0.0091 0.0056
0.0677 -0.0000 -0.0094
0.0677 -0.0000 0.0094
0.0675 0.0091 -0.0056
0.0675 0.0091 0.0056
0.0675 -0.0091 -0.0056
0.0675 -0.0091 0.0056
-0.0090 -0.0245 -0.0632
0.0090 -0.0245 -0.0632
-0.0091 -0.0150 -0.0661
0.0091 -0.0150 -0.0661
-0.0000 -0.0480 -0.0486
-0.0146 -0.0390 -0.0542
-0.0055 -0.0533 -0.0424
-0.0202 -0.0443 -0.0480
0.0146 -0.0390 -0.0542
0.0055 -0.0533 -0.0424
0.0202 -0.0443 -0.0480
-0.0181 -0.0206 -0.0626
-0.0237 -0.0353 -0.0536
0.0181 -0.0206 -0.0626
0.0237 -0.0353 -0.0536
0.0090 -0.0245 0.0632
-0.0090 -0.0245 0.0632
0.0091 -0.0150 0.0661
-0.0091 -0.0150 0.0661
0.0000 -0.0480 0.0486
-0.0146 -0.0390 0.0542
-0.0055 -0.0533 0.0424
-0.0202 -0.0443 0.0480
0.0146 -0.0390 0.0542
0.0055 -0.0533 0.0424
0.0202 -0.0443 0.0480
0.0181 -0.0206 0.0626
0.0237 -0.0353 0.0536
-0.0181 -0.0206 0.0626
-0.0237 -0.0353 0.0536
0.0090 0.0245 0.0632
-0.0090 0.0245 0.0632
0.0091 0.0150 0.0661
-0.0091 0.0150 0.0661
0.0000 0.0480 0.0486
-0.0146 0.0390 0.0542
-0.0055 0.0533 0.0424
-0.0202 0.0443 0.0480
0.0146 0.0390 0.0542
0.0055 0.0533 0.0424
0.0202 0.0443 0.0480
0.0181 0.0206 0.0626
0.0237 0.0353 0.0536
-0.0181 0.0206 0.0626
-0.0237 0.0353 0.0536
-0.0090 0.0245 -0.0632
0.0090 0.0245 -0.0632
-0.0091 0.0150 -0.0661
0.0091 0.0150 -0.0661
-0.0000 0.0480 -0.0486
-0.0146 0.0390 -0.0542
-0.0055 0.0533 -0.0424
-0.0202 0.0443 -0.0480
0.0146 0.0390 -0.0542
0.0055 0.0533 -0.0424
0.0202 0.0443 -0.0480
-0.0181 0.0206 -0.0626
-0.0237 0.0353 -0.0536
0.0181 0.0206 -0.0626
0.0237 0.0353 -0.0536
-0.0245 -0.0632 -0.0090
-0.0390 -0.0542 -0.0146
-0.0206 -0.0626 -0.0181
-0.0353 -0.0536 -0.0237
-0.0245 -0.0632 0.0090
-0.0390 -0.0542 0.0146
-0.0206 -0.0626 0.0181
-0.0353 -0.0536 0.0237
-0.0150 -0.0661 -0.0091
-0.0150 -0.0661 0.0091
-0.0480 -0.0486 -0.0000
-0.0443 -0.0480 -0.0202
-0.0533 -0.0424 -0.0055
-0.0443 -0.0480 0.0202
-0.0533 -0.0424 0.0055
-0.0245 0.0632 0.0090
-0.0390 0.0542 0.0146
-0.0206 0.0626 0.0181
-0.0353 0.0536 0.0237
-0.0245 0.0632 -0.0090
-0.0390 0.0542 -0.0146
-0.0206 0.0626 -0.0181
-0.0353 0.0536 -0.0237
-0.0150 0.0661 0.0091
-0.0150 0.0661 -0.0091
-0.0480 0.0486 0.0000
-0.0443 0.0480 -0.0202
-0.0533 0.0424 -0.0055
-0.0443 0.0480 0.0202
-0.0533 0.0424 0.0055
0.0245 0.0632 0.0090
0.0390 0.0542 0.0146
0.0206 0.0626 0.0181
0.0353 0.0536 0.0237
0.0245 0.0632 -0.0090
0.0390 0.0542 -0.0146
0.0206 0.0626 -0.0181
0.0353 0.0536 -0.0237
0.0150 0.0661 0.0091
0.0150 0.0661 -0.0091
0.0480 0.0486 0.0000
0.0443 0.0480 -0.0202
0.0533 0.0424 -0.0055
0.0443 0.0480 0.0202
0.0533 0.0424 0.0055
0.0245 -0.0632 -0.0090
0.0390 -0.0542 -0.0146
0.0206 -0.0626 -0.0181
0.0353 -0.0536 -0.0237
0.0245 -0.0632 0.0090
0.0390 -0.0542 0.0146
0.0206 -0.0626 0.0181
0.0353 -0.0536 0.0237
0.0150 -0.0661 -0.0091
0.0150 -0.0661 0.0091
0.0480 -0.0486 -0.0000
0.0443 -0.0480 -0.0202
0.0533 -0.0424 -0.0055
0.0443 -0.0480 0.0202
0.0533 -0.0424 0.0055
-0.0486 0.0000 -0.0480
-0.0542 -0.0146 -0.0390
-0.0424 -0.0055 -0.0533
-0.0480 -0.0202 -0.0443
-0.0542 0.0146 -0.0390
-0.0424 0.0055 -0.0533
-0.0480 0.0202 -0.0443
-0.0632 -0.0090 -0.0245
-0.0536 -0.0237 -0.0353
-0.0626 -0.0181 -0.0206
-0.0632 0.0090 -0.0245
-0.0536 0.0237 -0.0353
-0.0626 0.0181 -0.0206
-0.0661 -0.0091 -0.0150
-0.0661 0.0091 -0.0150
0.0486 0.0000 -0.0480
0.0542 -0.0146 -0.0390
0.0424 -0.0055 -0.0533
0.0480 -0.0202 -0.0443
0.0542 0.0146 -0.0390
0.0424 0.0055 -0.0533
0.0480 0.0202 -0.0443
0.0632 0.0090 -0.0245
0.0536 0.0237 -0.0353
0.0626 0.0181 -0.0206
0.0632 -0.0090 -0.0245
0.0536 -0.0237 -0.0353
0.0626 -0.0181 -0.0206
0.0661 0.0091 -0.0150
0.0661 -0.0091 -0.0150
0.0486 -0.0000 0.0480
0.0542 -0.0146 0.0390
0.0424 -0.0055 0.0533
0.0480 -0.0202 0.0443
0.0542 0.0146 0.0390
0.0424 0.0055 0.0533
0.0480 0.0202 0.0443
0.0632 0.0090 0.0245
0.0536 0.0237 0.0353
0.0626 0.0181 0.0206
0.0632 -0.0090 0.0245
0.0536 -0.0237 0.0353
0.0626 -0.0181 0.0206
0.0661 0.0091 0.0150
0.0661 -0.0091 0.0150
-0.0486 -0.0000 0.0480
-0.0542 -0.0146 0.0390
-0.0424 -0.0055 0.0533
-0.0480 -0.0202 0.0443
-0.0542 0.0146 0.0390
-0.0424 0.0055 0.0533
-0.0480 0.0202 0.0443
-0.0632 -0.0090 0.0245
-0.0536 -0.0237 0.0353
-0.0626 -0.0181 0.0206
-0.0632 0.0090 0.0245
-0.0536 0.0237 0.0353
-0.0626 0.0181 0.0206
-0.0661 -0.0091 0.0150
-0.0661 0.0091 0.0150
-0.0182 0.0000 -0.0659
-0.0273 -0.0056 -0.0624
0.0182 0.0000 -0.0659
0.0273 -0.0056 -0.0624
-0.0273 0.0056 -0.0624
0.0273 0.0056 -0.0624
-0.0056 -0.0624 -0.0273
0.0056 -0.0624 -0.0273
-0.0351 -0.0442 -0.0386
-0.0386 -0.0351 -0.0442
-0.0000 -0.0659 -0.0182
-0.0442 -0.0386 -0.0351
0.0351 -0.0442 -0.0386
0.0386 -0.0351 -0.0442
0.0442 -0.0386 -0.0351
0.0182 -0.0000 0.0659
0.0273 -0.0056 0.0624
-0.0182 -0.0000 0.0659
-0.0273 -0.0056 0.0624
0.0273 0.0056 0.0624
-0.0273 0.0056 0.0624
-0.0056 -0.0624 0.0273
0.0056 -0.0624 0.0273
-0.0351 -0.0442 0.0386
-0.0386 -0.0351 0.0442
-0.0000 -0.0659 0.0182
-0.0442 -0.0386 0.0351
0.0351 -0.0442 0.0386
0.0386 -0.0351 0.0442
0.0442 -0.0386 0.0351
-0.0056 0.0624 0.0273
0.0056 0.0624 0.0273
-0.0351 0.0442 0.0386
-0.0386 0.0351 0.0442
-0.0000 0.0659 0.0182
-0.0442 0.0386 0.0351
0.0351 0.0442 0.0386
0.0386 0.0351 0.0442
0.0442 0.0386 0.0351
-0.0056 0.0624 -0.0273
0.0056 0.0624 -0.0273
-0.0351 0.0442 -0.0386
-0.0386 0.0351 -0.0442
-0.0000 0.0659 -0.0182
-0.0442 0.0386 -0.0351
0.0351 0.0442 -0.0386
0.0386 0.0351 -0.0442
0.0442 0.0386 -0.0351
-0.0624 -0.0273 -0.0056
-0.0624 -0.0273 0.0056
-0.0659 -0.0182 -0.0000
-0.0624 0.0273 -0.0056
-0.0624 0.0273 0.0056
-0.0659 0.0182 -0.0000
0.0624 0.0273 -0.0056
0.0624 0.0273 0.0056
0.0659 0.0182 0.0000
0.0624 -0.0273 -0.0056
0.0624 -0.0273 0.0056
0.0659 -0.0182 0.0000

GIBBON www.gibboncode.org
Kevin Mattheus Moerman, [email protected]
GIBBON footer text
License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE
GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.
Copyright (C) 2019 Kevin Mattheus Moerman
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.